【一級建築士】構造と力学の勉強方法と超基本を解説（点数UPに直結）

この記事はこのような方に向けて書いています↓

　この記事の筆者は、2020年の学科試験で105点（125点満点）を獲得し、合格しています。合格点は88点でしたので、17点の余裕をもって合格しています。

　学習期間は1年程度。

　初年度の製図試験は不合格。2021年に2回目の製図試験で合格しました。

一級建築士の独学には、模試の活用が重要です。模試についての記事もあるので参考にしてください。

【一級建築士　独学】模試を受けよう！メリットと注意点を解説

「一級建築士試験の模試について知りたい」、「一級建築士試験の模試を受けたら点数が悪かった、、、」といった方に向けた記事です。一級建築士試験の模試を受けるメリット、模試の種類と難易度、模試を受けた後にすべきことを解説します。

kenchikuojisan-dokugaku.com

2021.03.28

構造力学の勉強方法

構造力学でも過去問演習の繰り返しが重要

　構造力学でも、他の科目と同様、過去問演習の繰り返しが重要です。

　過去問演習をする中で解き方の流れを覚えていくイメージです。解き方のバリエーションが少ないので得点源となりやすいです。

　学科Ⅳ構造では、初めて見るような問題でも、すでに持っている知識から解けることも多いです。これは、他の教科でも言えることですが、構造だとより当てはまります。

　最初は解けない問題だらけと思いますが、心配は要りません。

　解けない問題は、まずは解答解説の解き方を真似するのが大事です。

　解答解説の解き方の流れが分かったら、解答を見ずに再現してみます。

　解けない問題に遭遇するたびにこれを繰り返すことで、解ける問題が増えていきます。

構造力学の問題をある程度こなしたら、解けなかったときや間違えたときに抱く感覚に注目する

　構造力学の問題をある程度こなして、解き方の流れが身についてきたら、正答できる問題が増えていくはずです。

　それでも正答できない問題や解き方が分からない問題もあると思います。

　その時は、下の１と２のどちらの感想を抱くかで、今後の対応が違ってきます。

1. 解答解説で出てくる知識は全て知っていた。こんな問題だったら解けたなあ。
2. 知らなかった知識があったから、この問題は今の自分では解けない

　１の感想を抱いた人は、知識が身に付いてきた証拠です。

　難しい問題に遭遇したときに、安易に諦めて解答解説を見るのではなく、知っている知識で解く努力をして粘ってみるようにしましょう。

　２の感想を抱いた人は、まだインプットが足りていません。

　より多くの問題に触れて、解き方のパターンを覚えていきましょう。

　そのとき、

まずは自分で解いてみる→解けなかった問題は、解答解説の解き方を真似して解く→解答解説を見ずに解き方を思い出しながら解く

　を必ず実践するようにしてください。

構造力学の重要性

　一級建築士試験の学科Ⅳ構造では、毎年必ず５～６問の構造力学の問題（←計算問題）が出ます。

　構造力学の問題は、必ず満点を取れるレベルにしておきたい問題です。

　理由はこの通りです↓

　構造力学は、1つ１つの解き方、考え方の結びつきが強いので、最初は問題を解くのが難しく感じるかもしれませんが、問題の解き方の流れ（パターン）を一通り覚えたら、少ない知識でも得点できます。

一級建築士構造で大事な超基本4つ

　この章で伝えることを理解できているかどうかで、学習効率と点数に雲泥の差が出ます。とても大事な内容なので、ぜひ読んでみてください。

　そして、読んでみた後は必ず過去問や問題を解いてみてください。この記事で得た知識が生きるはずです。

　特に構造力学の問題を解いていて行きづまっている人には、とても役立つ内容です。

力とモーメントのつり合いと反力

力のつり合い

　物体が静止しているとき、物体にかかっている力はつり合っています。　

　つり合っているというのは、右向きの力の合計＝左向きの力の合計となっており、かつ、上向きの力の合計＝下向きの力の合計となっているイメージです。

　（正確には、左回りのモーメントの合計＝右回りのモーメントの合計にもなっています。）

　力がつり合っていないときは、物体は動きますし、モーメントがつり合っていないときは、物体は回ります。

　いくつかイラストで例を示してみたいと思います。

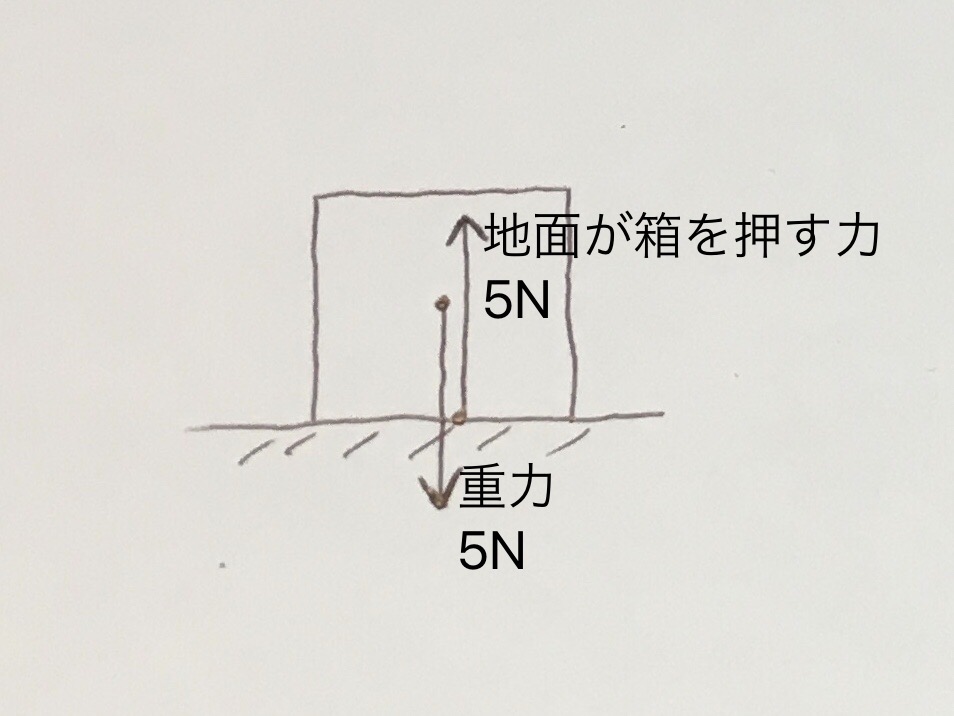
　上図では、箱が静止している状態です。

　この時箱に５N（５ニュートン）の重力がかかっているとすると、箱は地面から、重力と逆向きに5Nの力を受けています。

　上向きの力の合計＝下向きの力の合計となっているので、力がつり合って静止しているというわけです。

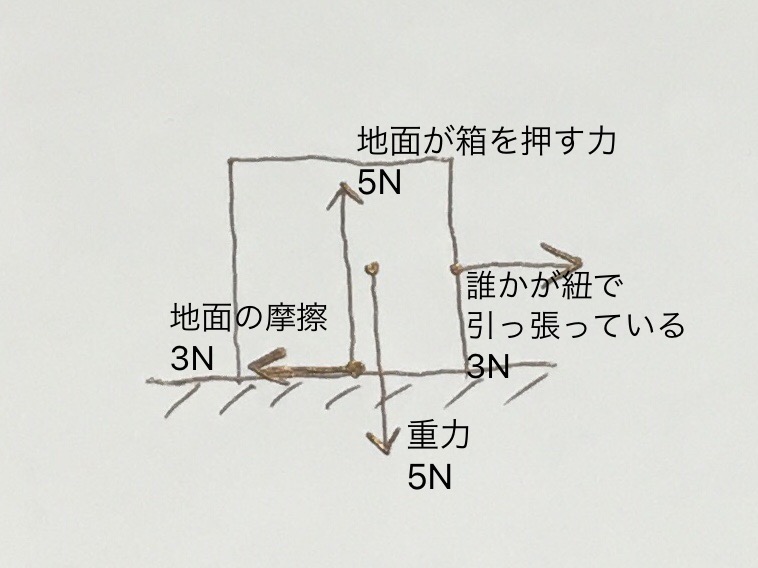
　上図では、さきほど登場した箱を、誰かが３Nの力で引っ張っているけど、動いていない状態です。

　動いていないということは、力がつり合っているということなので、誰かが引っ張る３Nの力の逆向きに、地面から３Nの摩擦力を受けていることになります。

　上向きの力の合計＝下向きの力の合計、かつ、左向きの力の合計＝右向きの力の合計　となっているため、力がつり合って静止しているというわけです。　

　ここからは、縦方向の力は、上向きを＋（プラス）、下向きを－（マイナス）で表すことにしましょう。

　すると、上図の状態は、縦方向の力について、（＋５N）＋（－５N）＝０となっていることが分かります。力がつり合っているとき、上向きを＋（プラス）、下向きを－（マイナス）で表すと、縦方向の力の合計が０になるということです。

　また、同じように、横方向の力は、右向きを＋（プラス）、左向きを-（マイナス）で表すことにしましょう。

　すると、上図の状態は、横方向の力について、（＋３N）＋（-３N）＝０となっていることが分かります。力がつり合っているとき、右向きを＋（プラス）、左向きを-（マイナス）で表すと、横方向の力の合計が0になるということです。

　このように、力がつり合っている（＝静止している）物体は、縦方向の力の合計が０、かつ、横方向の力の合計が０となります。

　上図の説明では省略しますが、正確には、縦方向と横方向の力だけでなく、「モーメント」も、つり合っています。

　モーメントのつり合いについては次の図で説明します。また、モーメントが何なのかについては、後ほど解説しますので、ぜひ最後まで読んでください。

モーメントのつり合い

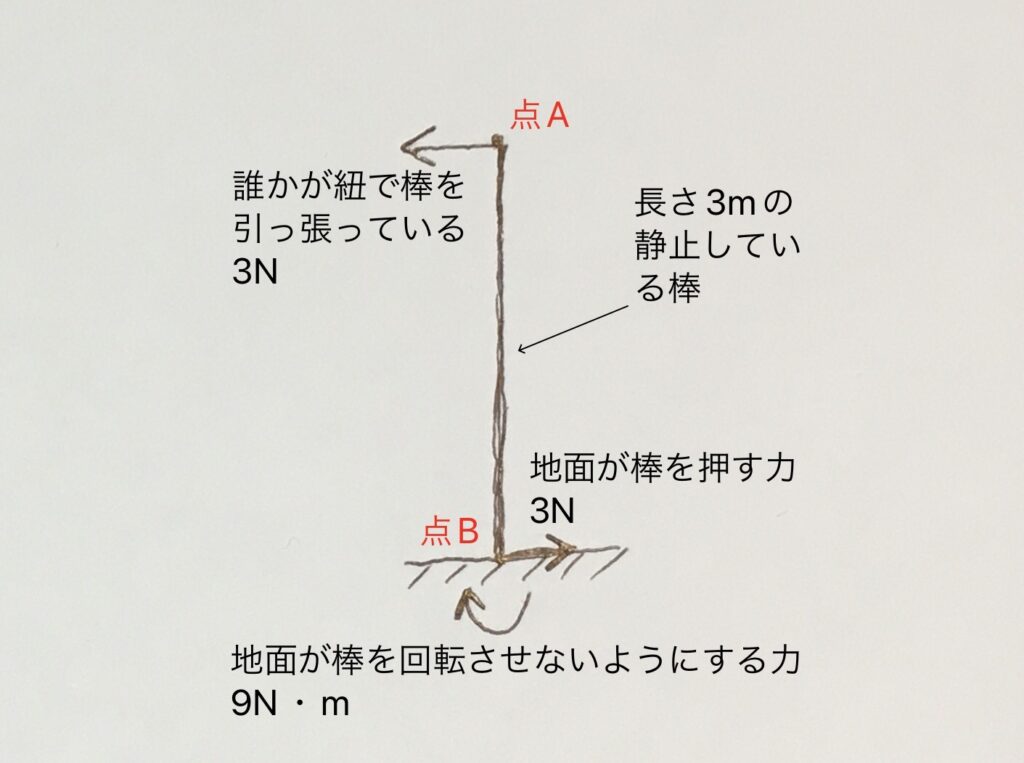
　上図は、長さ３ｍの棒が地面に固定されていて、その一番上の先っちょ（点A）を、誰かが３Ｎの力で左向きに引っ張っているが、棒は動いていない状態です。（重力については考えず、省略しています）

　この時、棒が動いていないということは力がつり合っており、横向きの力の合計は０となるはずなので、地面が棒を右向きに３Nの力で押していることになります。

　そしたら、（＋３N）＋（-３N）＝０となりますよね。

　でも、地面から棒に加わっている力が右向きの力３Nだけでは違和感を感じませんか？

　上図のように、右向きに３N、左向きに３Nの力が働いていたら、棒は、点Bを中心に左に倒れそうですよね。

　ここで、「モーメント」が登場します。

　モーメントが何なのかについては後ほど詳しく説明しますが、ここでは、モーメントのつり合いについて理解してください。

　モーメントというのは、簡単に言うと回転させようとする力です。

　モーメントの大きさは、かかっている力の大きさと、ある地点（今回は点B ）から、力（今回は点A）までの距離を掛け算した値となります。

　上図では、点Bから３ｍ離れた位置にある、点Ａに３Ｎの左向きの力がかかっていますので、

３×３＝９Ｎ・ｍ（ニュートンメートル）の大きさの、左回転のモーメントが、点Bには生じています。

　でも棒は回転せずに静止しているわけですから、棒は、地面から点Bに、右回転の９N・ｍのモーメントを受けていることになります。

　左回転のモーメントの合計＝右回転のモーメントの合計となるので、静止している（＝モーメントがつり合っている）というわけです。

　そしてここからは、左回転のモーメントを＋（プラス）、右回転のモーメントを－（マイナス）で表すこととしましょう。

　すると、上図では、（＋９N・ｍ）＋（-９Ｎ・ｍ）＝０となります。

　これが、モーメントがつり合っている状態です。左回転のモーメントを＋（プラス）、右回転のモーメントを－（マイナス）で表したときに、モーメントの合計が0となっています。

モーメントがつり合っているとき、どの点を中心に考えてもモーメントの合計は０となる

　ここで、モーメントのつり合いについて、大事なことを伝えます。

　モーメントのつり合いを考えるときは、力のつり合いを考える時と違い、ある「点」にかかるモーメントについて考えます。

　力のつり合いを考えるときは、「棒」にかかっている横向きの力の合計＝０、かつ、「棒」にかかっている縦向きの力の合計＝０でしたよね。

　でも、モーメントのつり合いを考えるときは、「点B」を中心としたモーメントの合計＝０という考え方でした。これがモーメントの大事な特徴です。

　また、ある点を中心としたモーメントの合計が０のとき、他の点を中心としたモーメントの合計も必ず０となります。

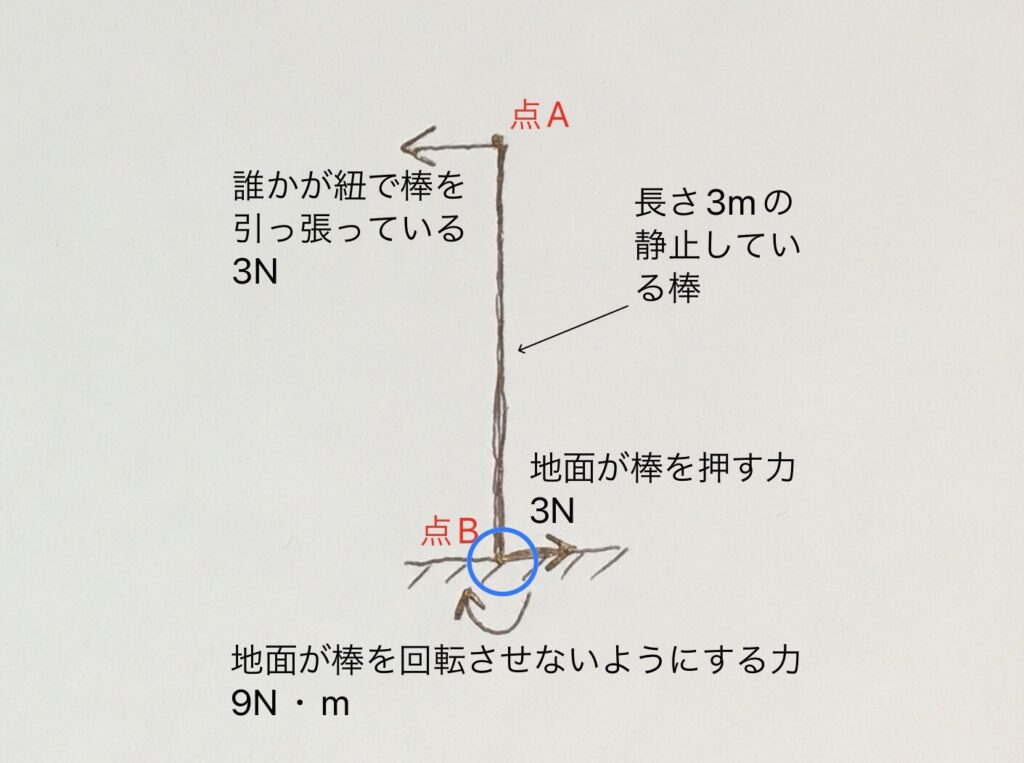
　上図では、点Bを中心としたモーメントの合計が０となりましたが、点Aを中心としたモーメントの合計も０となりますので、計算してみましょう。

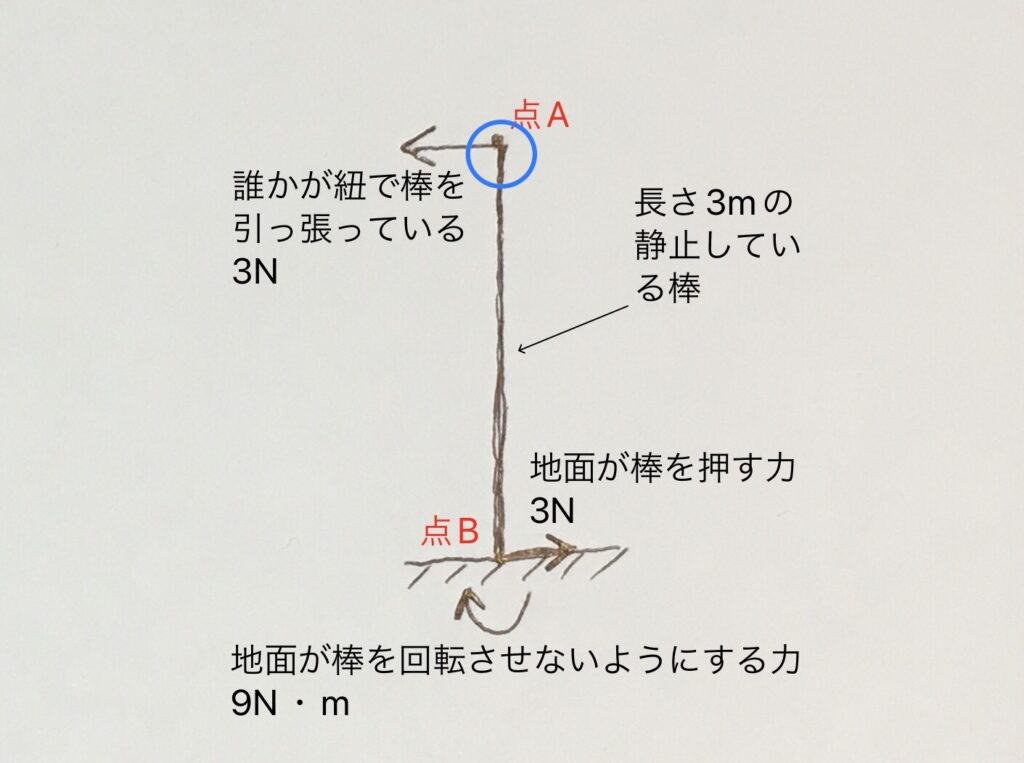
　まず、点Aに左向きの３Nの力がかかっていますが、点Aを中心に考えると、点Aから左向きの力まで距離が０なので、モーメントは３N×０ｍ＝０です。

　次に、点Bに右向きの３Nの力がかかっており、点Aから右向きの力までの距離は３ｍなので、３Ｎ×３ｍ＝９Ｎ・ｍとなり、点Aを中心とした左回転のため、符号は＋（つまり＋９N・ｍ）です。

　また、点Bには地面から９N・ｍのモーメントがかかっており、こちらは右回転のモーメントなので符号は-（つまり-９N・ｍ）です。

　合計すると、０＋（＋９N・ｍ）＋（-９Ｎ・ｍ）＝０となりました。

　点Aや点B以外の、別の点（例えば棒の真ん中）を中心としたモーメントを計算しても、結果は同じになります。

モーメントは「力の大きさ」×「力までの距離」で算定されるが、「力までの距離」とは力までの最短距離のこと

　もう１つ、モーメントについて考えるときに大事なことを伝えます。

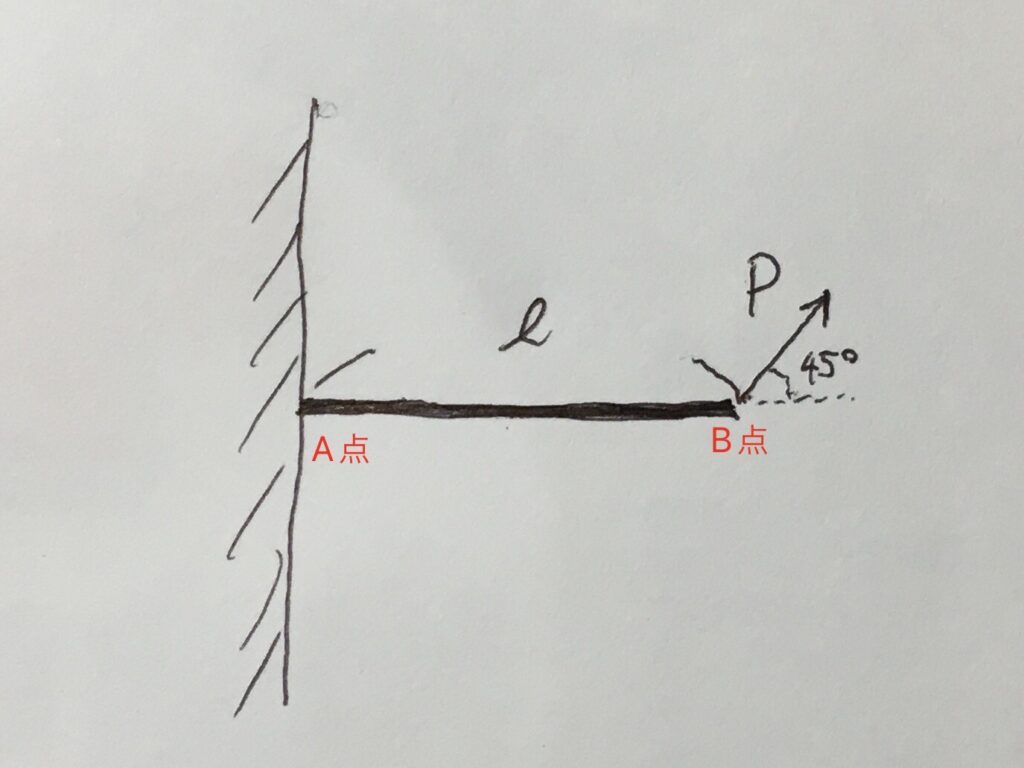
　長さℓの梁の先っちょに、斜め45度の方向に大きさPの力が働いています。

　この時、A点を中心としたモーメントはどのようになっているでしょうか。

　P×ℓ＝Pℓ　ではありません！

　

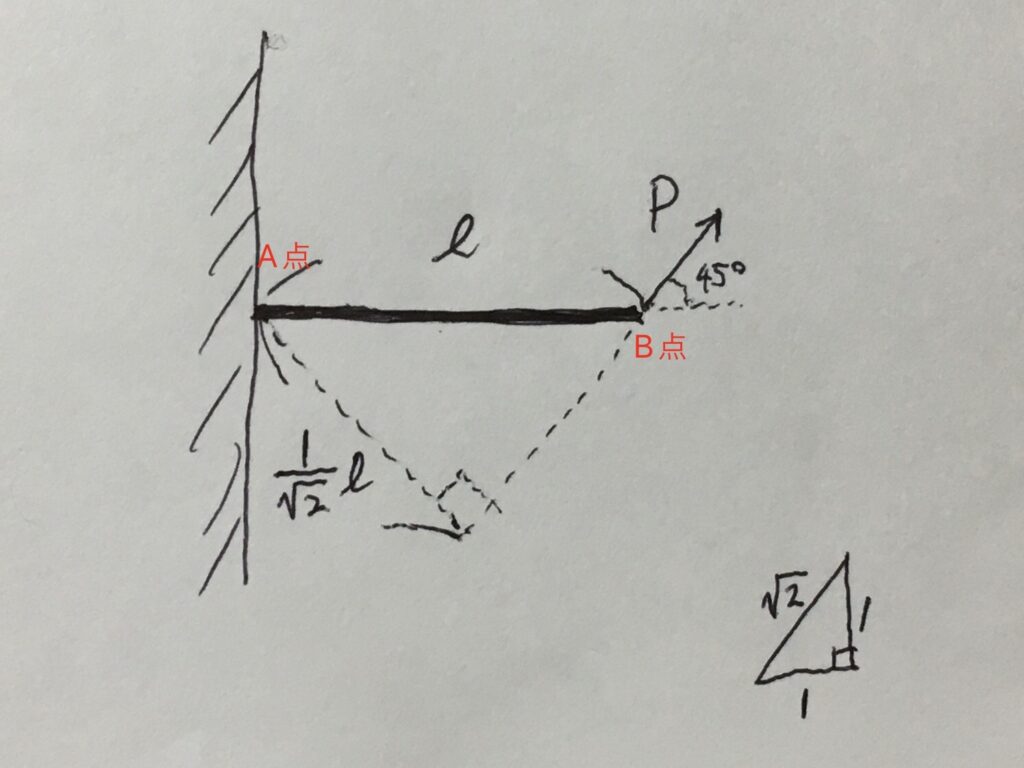
　力が斜めに働いているときは、「A点から力までの距離」は、力の直線を延長して直角に交わったところの距離（＝最短距離）となります。

　今回は斜め45度の方向に力が働いていたため、力までの距離は（１/√2）ℓです。

　そのため、A点を中心としたモーメントは、（１/√２）Pℓとなります。

反力とは地面などが物体（建物）を支える力

　図１～図３では、箱や棒に対して地面から力がかかっていましたね。

　図1では上向きの力５N、図2では上向きの力５Nと左向きの力３N、図3では右向きの力３Nと右回転のモーメント９N・ｍによって、地面から支えられていました。

　これらの支える力を反力と呼びます。

　物体が地面以外にも接していて支えられている場合は、地面以外からも物体に対して反力がかかっています。

　例えば、物体が地面と壁に接して支えられている場合は、壁と地面から反力を受けています。

　下の図が、その例です。

　壁と地面から受けている、箱を支えている力（右向き２N、右向き１N、上向き５N）が反力です。

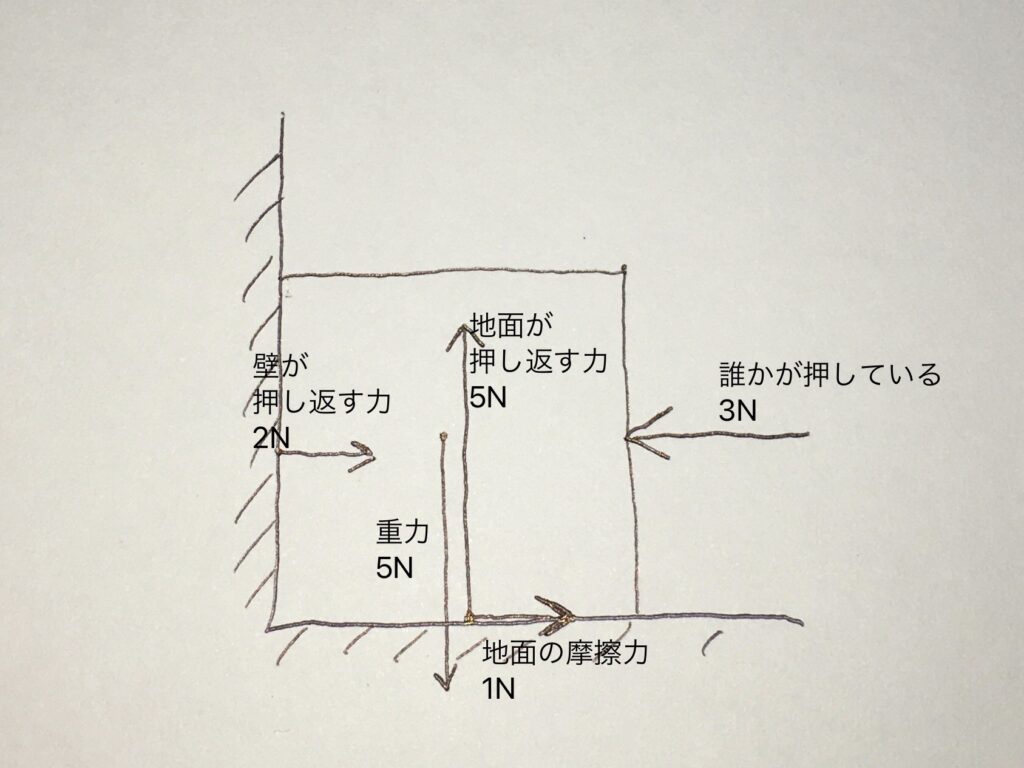
　構造力学の問題の8割くらいは、まず一番初めに地面や壁からの反力を計算します。

建物の支持の種類：ピン、ローラー、剛

　直前のセクションで説明したとおり、建物（物体）を、地面や壁が支える力を反力と呼びますが、建物が受ける反力の種類（縦向きの力or横向きの力orモーメント）は、支持の種類によって異なります。支持の種類というのは、建物がどのように地面や壁から支えられているのか　です。

　部材がピン支持・ローラー支持・剛支持によって支えられているそれぞれのイメージを、下図に示します。

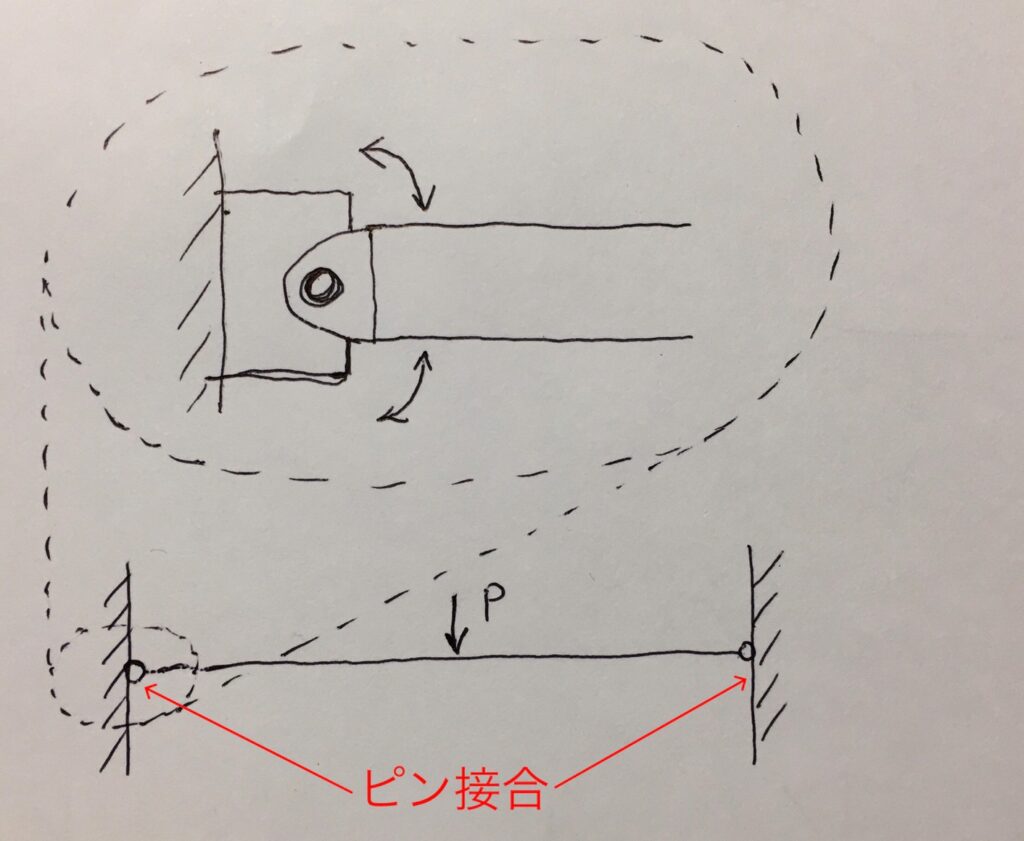
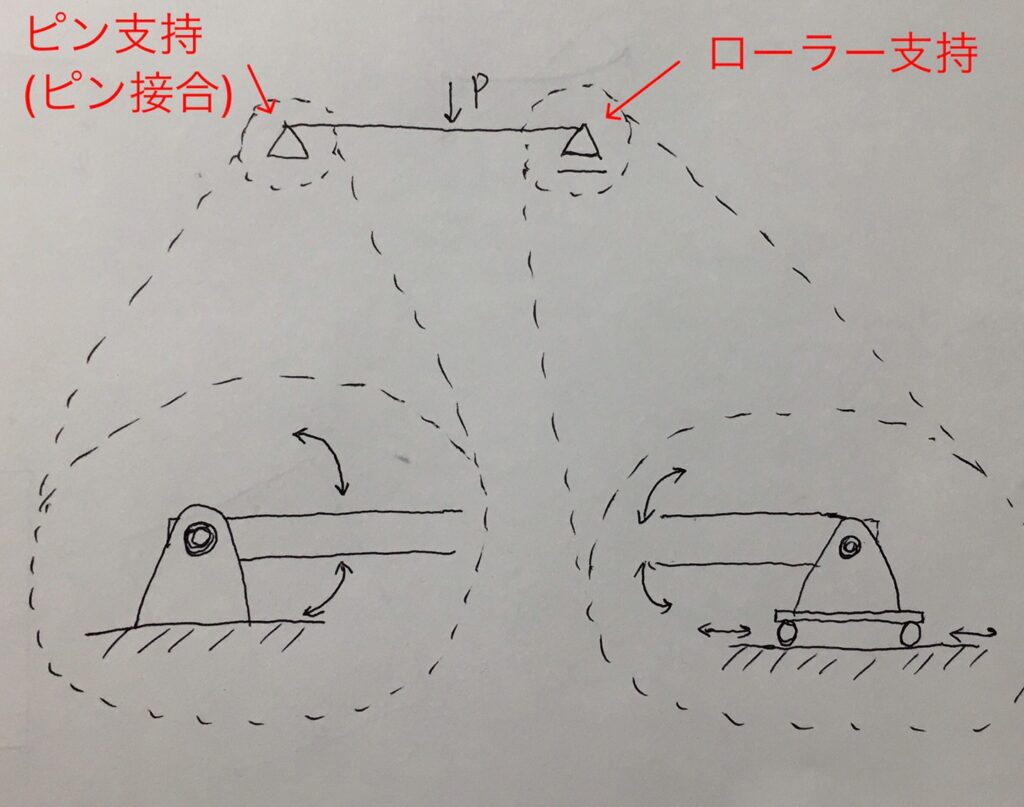
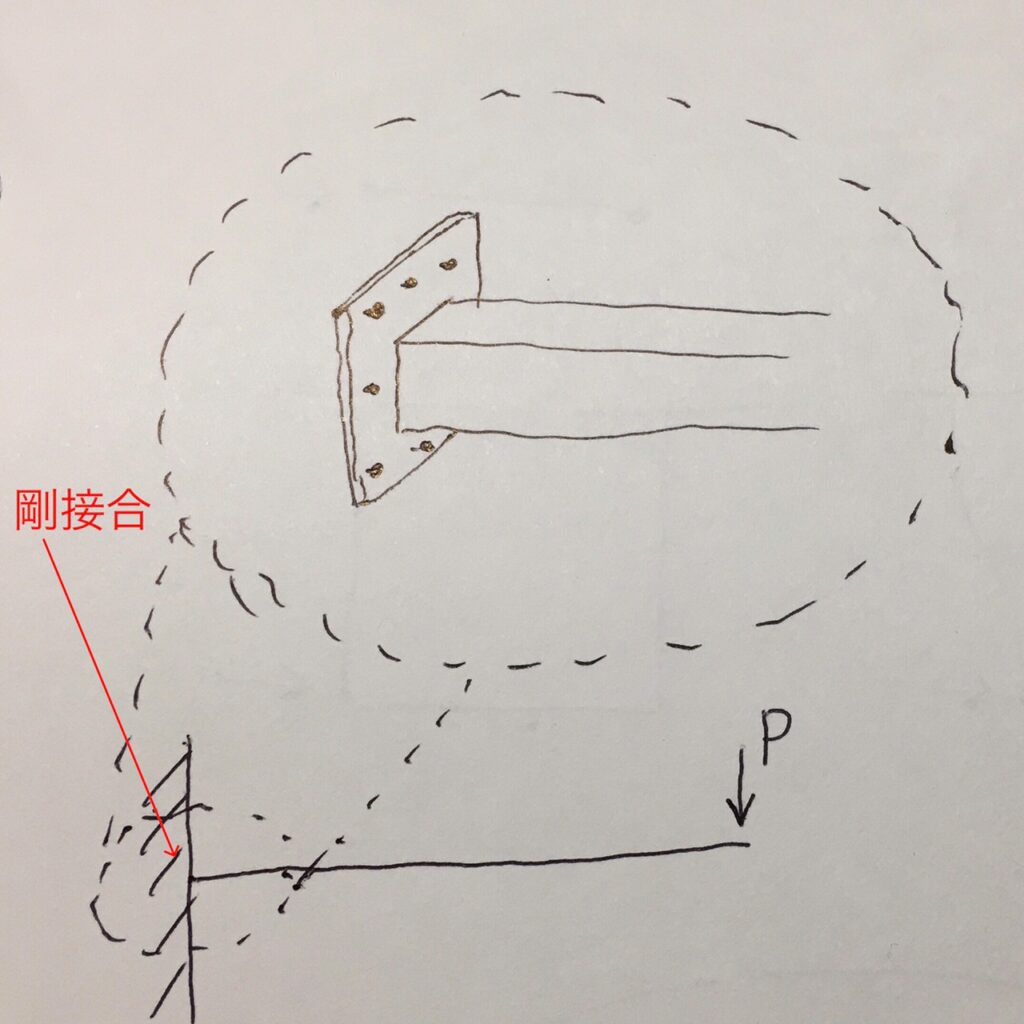
　図５と図6からわかる通り、ピン支持の場合、部材は上下にも左右にも動きませんが、回転させることはできます。

　図６からわかる通り、ローラー支持の場合、部材は上下には動きませんが、左右に動かしたり回転させたりすることはできます。

　図７からわかる通り、剛支持の場合、部材は上下にも左右にも動かず、回転させることもできません。

• 動かせない（回転できない）＝反力を受けている
• 動かせる（回転できる）＝反力を受けていない

ということですので、以下のことが言えます。

モーメントは回転させようとする力。モーメントのイメージを解説。

　これまでに何度か出てきた、「モーメント」について説明します。

　モーメントは、スパナ🔧でナットを回転させるときや、てこで重いものを持ち上げるときをイメージしたらわかりやすいです。

　中心から離れたところに力を加えた方が、大きな力を加えることができますよね。

　「てこの原理」が、まさしくモーメントの考え方を使っています。

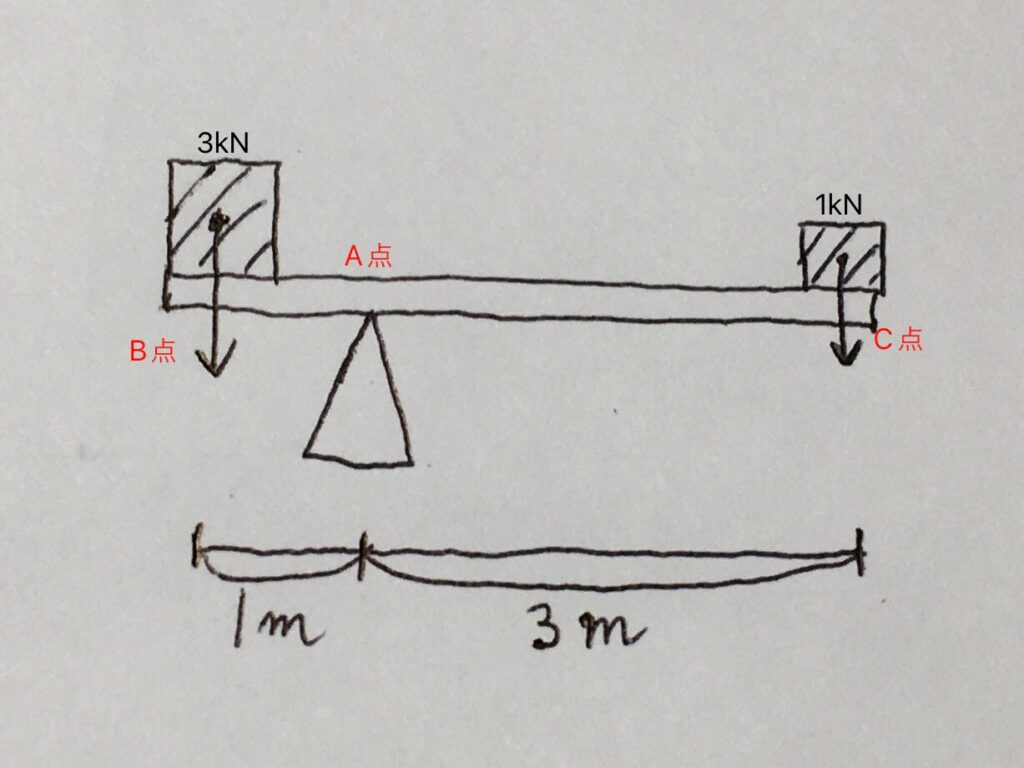
　上図では、シーソーがつり合っており右側にも左側にも動きませんが、それは、A点（支点）を中心としたモーメントがつり合っているからです。

　左回転のモーメントを＋、右回転のモーメントをーで表すと、A点を中心としたモーメントについて、

【＋（３ｋＮ×１ｍ）】＋【ー（１ｋＮ×３ｍ）】＝０

となっていることが分かります。

　モーメントがつり合っているときは、左回転のモーメントを＋、右回転のモーメントをーで表したときの、モーメントの合計が０となります。

　次は、モーメントをよりイメージしてもらうため、部材で説明します。

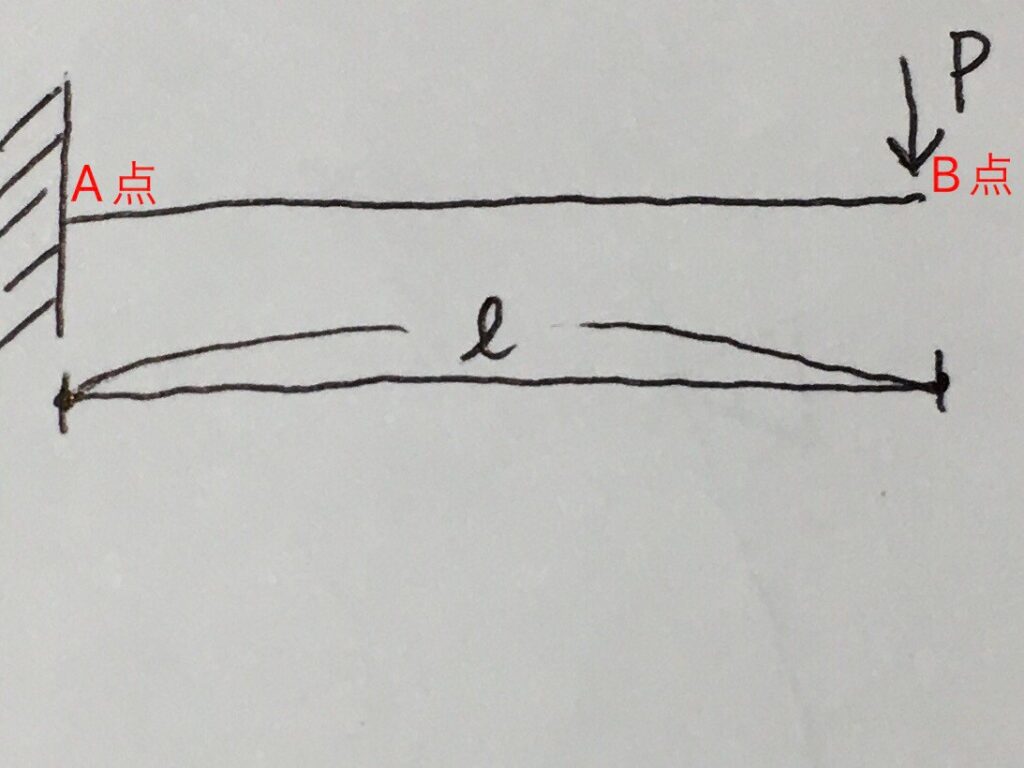
　上図は、壁から梁が突き出ているようなイメージです。

　こんな梁を片持ち梁と言います。

　長さはℓで、先っちょに大きさＰの力がかかっています。

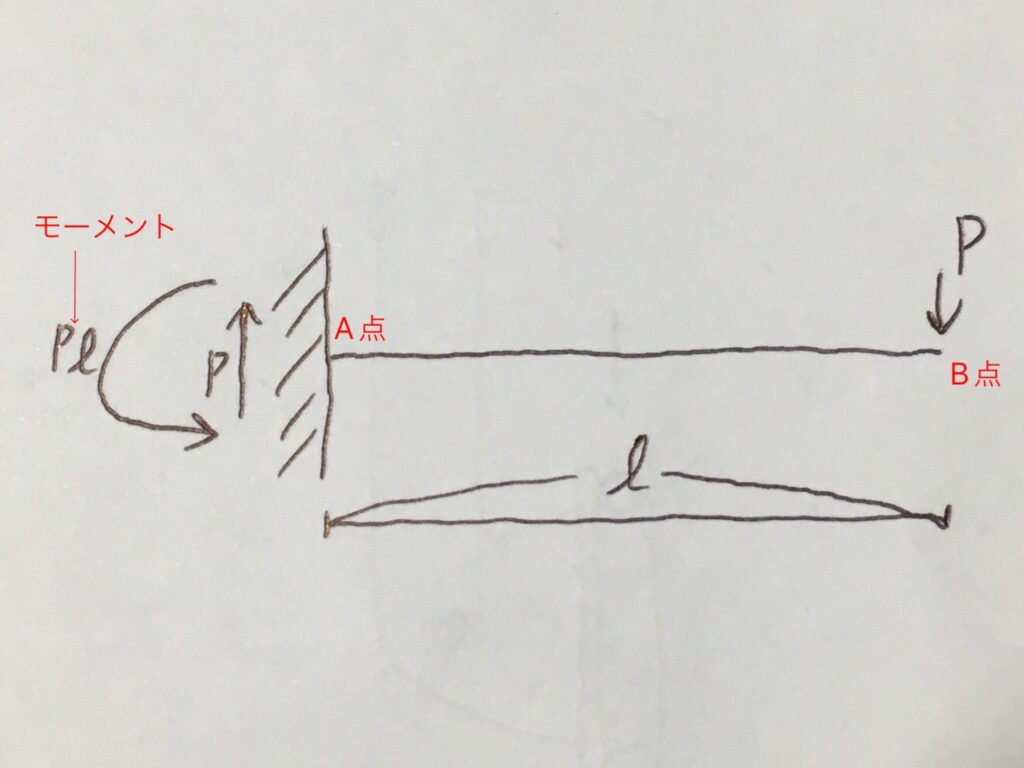
　この時、梁は静止しており、動いたり回転したりしていませんので、力とモーメントがつり合っています。

　つまり、下に押す力Pに対抗するため、壁から梁に上向きの反力Pが加わっています。

（＋P）＋（ーP）＝０

　また、A点を中心に右回転させようとするモーメントPℓ🔁（B点にかかっている力P×A点からの距離ℓ）に対抗するため、壁から梁に左回転の反力モーメントPℓ🔄が加わっています。

（＋Pℓ）＋（ーPℓ）＝０

　壁から梁に加わる反力モーメントPℓについて、まだイメージしにくいと思うので、もしも反力モーメントがなかったらどうなるかについて考えてみます。　

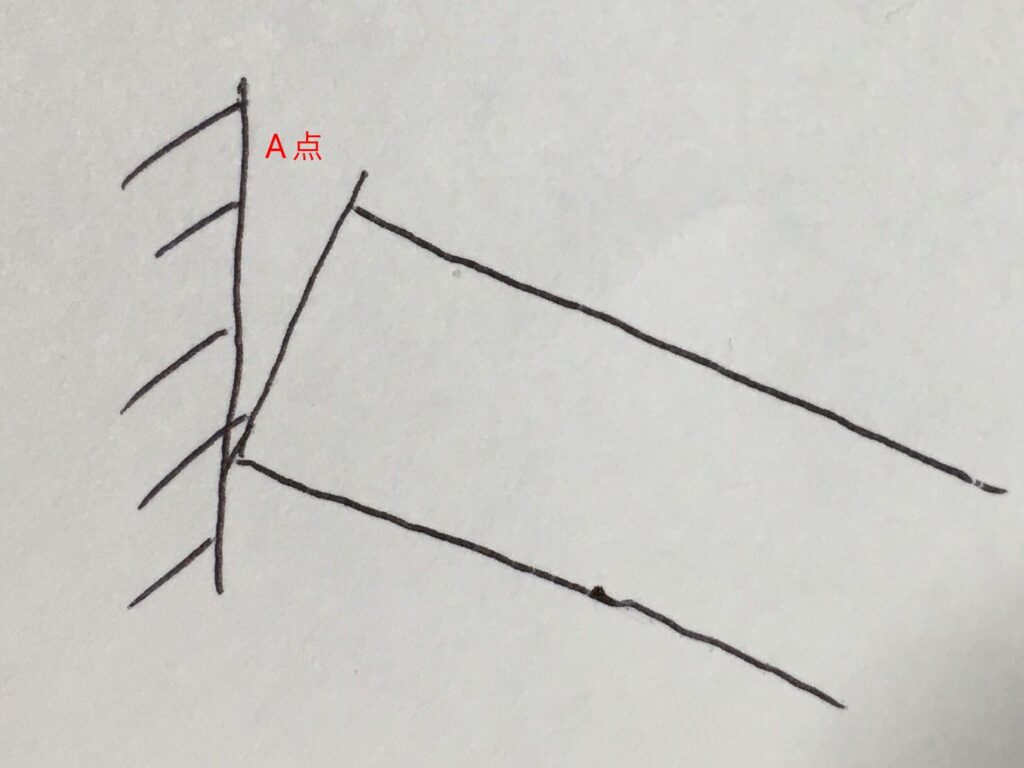
　もし反力モーメントがなかったら、上図のように、ポッキリと根元から梁が折れてしまいます。

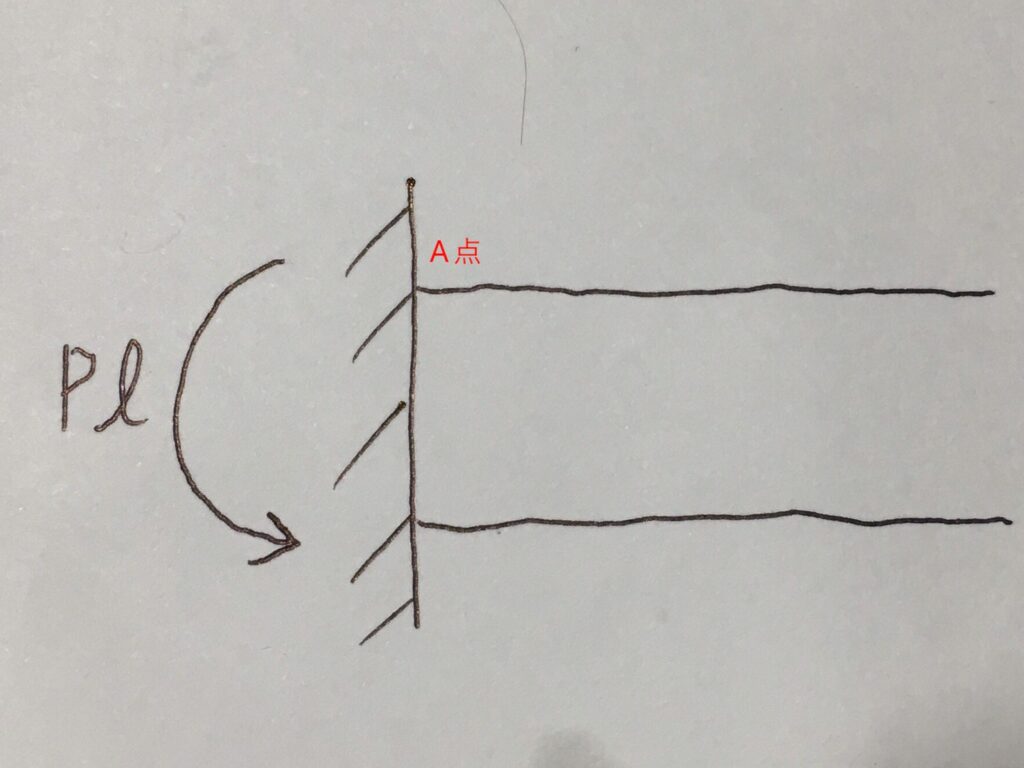
　上図のように左向きの反力モーメント🔄が壁から梁に加わっているため、ポッキリとならずに済んでいるわけです。

　もっとイメージしやすくするため、反力モーメントPℓの正体について考えてみます。

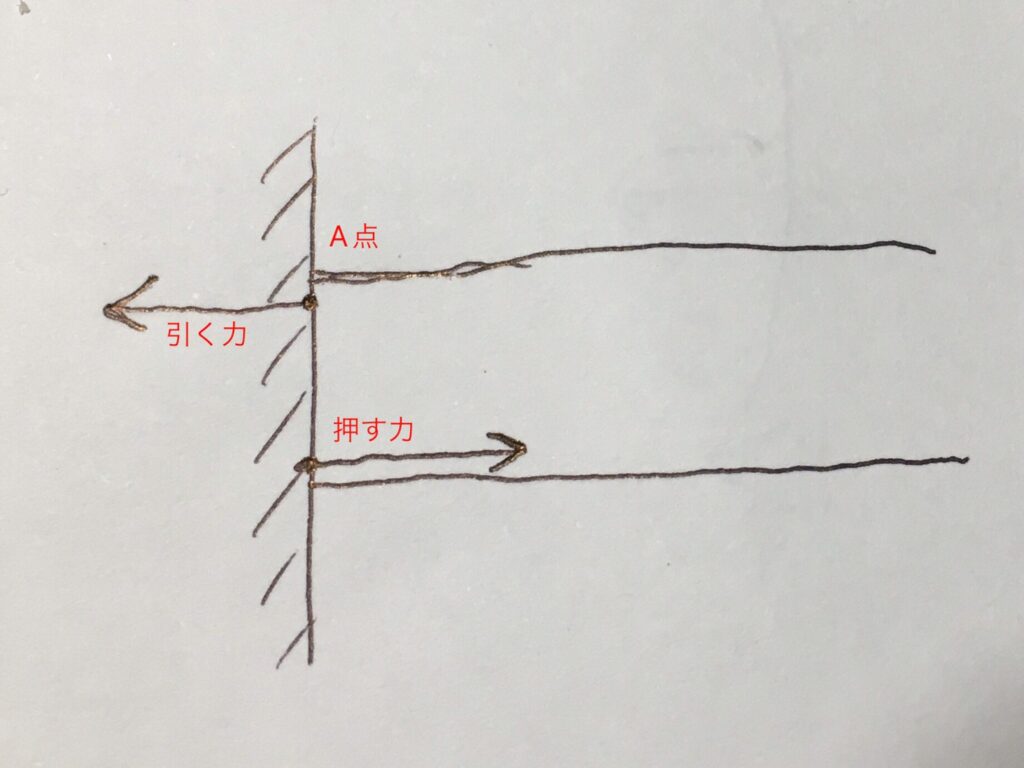
　反力モーメントPℓの正体は、上図のような、大きさが等しい、押す力と引く力の組み合わせです。

　上の引く力が、梁の根元の上半分が壁から剥がれないように対抗し、下の押す力が、梁の根元の下半分が壁にめり込まないように対抗しています。

　（上図では引く力と押す力がそれぞれ1つの点に加わっていますが、実際は壁と接している面全体に押す力と引く力が加わっています。ここではモーメントをイメージしてもらうため、簡略化して図示しています。）

　このような、大きさが等しい反対向きの力の組み合わせを偶力といい、構造力学の問題の中でもたまに出てきます。

　「反力モーメントの正体は押す力と引く力の組み合わせ」と覚えておきましょう。

応力の算定・モーメント図のコツ

　部材が力を受けると、部材の内部に応力という力が発生します。

　部材のどの部分にどの程度の大きさの応力が発生するかを計算することで、部材に力が加わったときにどの部分が一番先に折れるかを予測することができます。

　均一な太さの部材なら、当然、一番大きな応力が発生している部分が一番折れやすいです。

　例えば、上図の梁で一番先に折れやすそうなのはどの部分か、考えてみましょう。

　一番根元のA点で折れそうですよね。

　B点でも梁の中間でもなく、A点で折れそうだと思った人は、A点に発生する応力が、梁の他の部分に発生する応力よりも最も大きいということを、直感的に理解していることになります。

　応力には3種類（軸力・せん断力・曲げモーメント）がありますが、上図の場合は、A点で曲げモーメントが最も大きいため、A点で折れやすくなります。

軸力・せん断力・曲げモーメントのイメージ

　部材が力を受けると、部材の内部に応力という力が発生することを説明しました。部材が外部から力を受けていないときには、応力は発生しません。

　応力には3種類（軸力・せん断力・曲げモーメント）がありました。

　軸力とは、部材と平行に生じる力で下図のような場合に部材の内部に生じているイメージです。

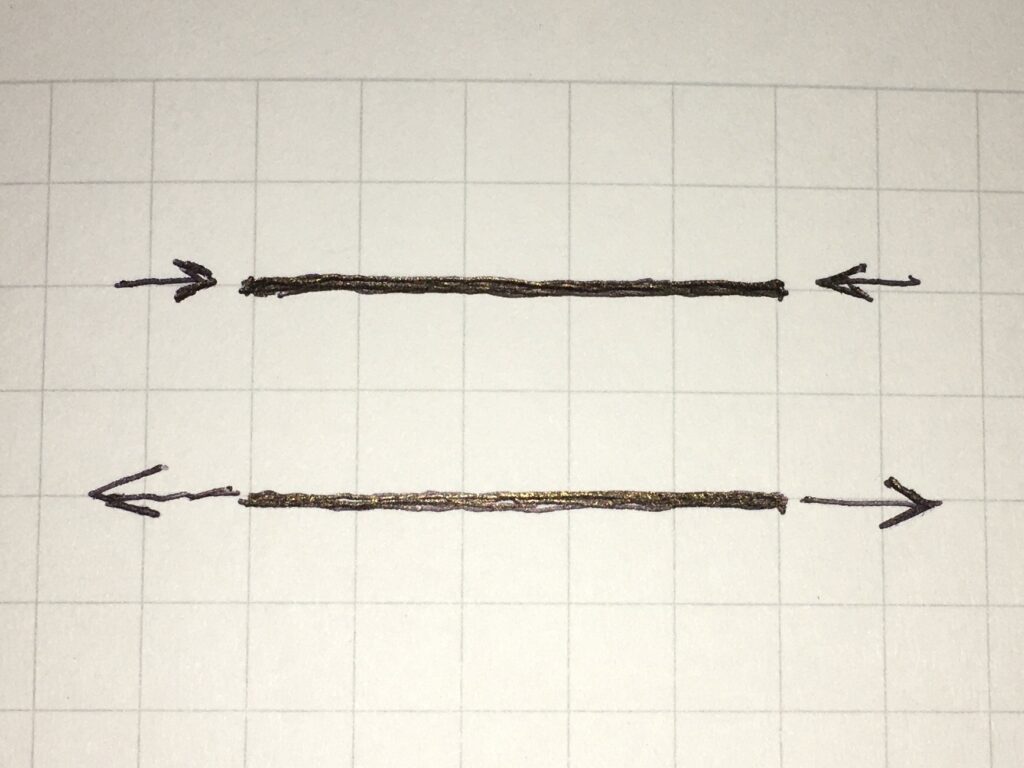
　せん断力とは、部材と垂直方向に生じる力です。外部からかかる力が大きいと、それに伴ってせん断力も大きくなります。外部からかかる力が大きすぎると、発生したせん断力によって、下図のように部材がちぎれます。

　折れるわけではなく、ちぎれるようなイメージを持ってください。

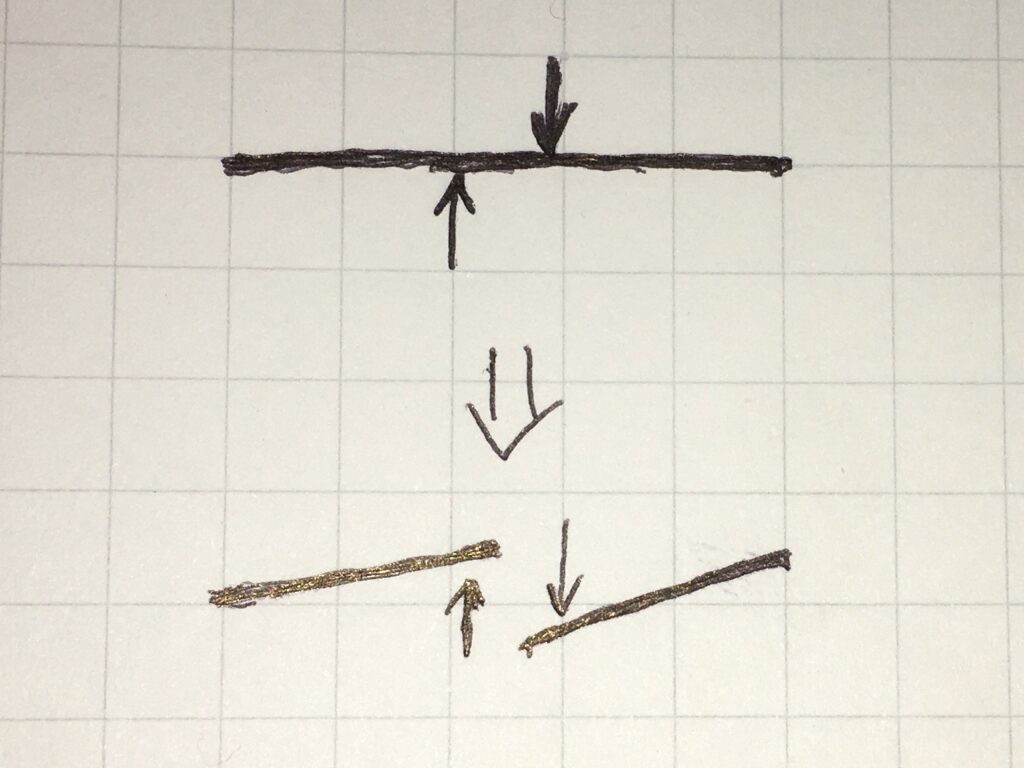
　曲げモーメントは、部材の内部に生じているモーメントです。外部からかかる力が大きいと、それに伴って曲げモーメントも大きくなります。外部からかかる力が大きすぎると、発生した曲げモーメントによって、下図のように部材ポキリと折れます。

　ちぎれるわけではなく、曲がって折れるというイメージを持ってください。

　

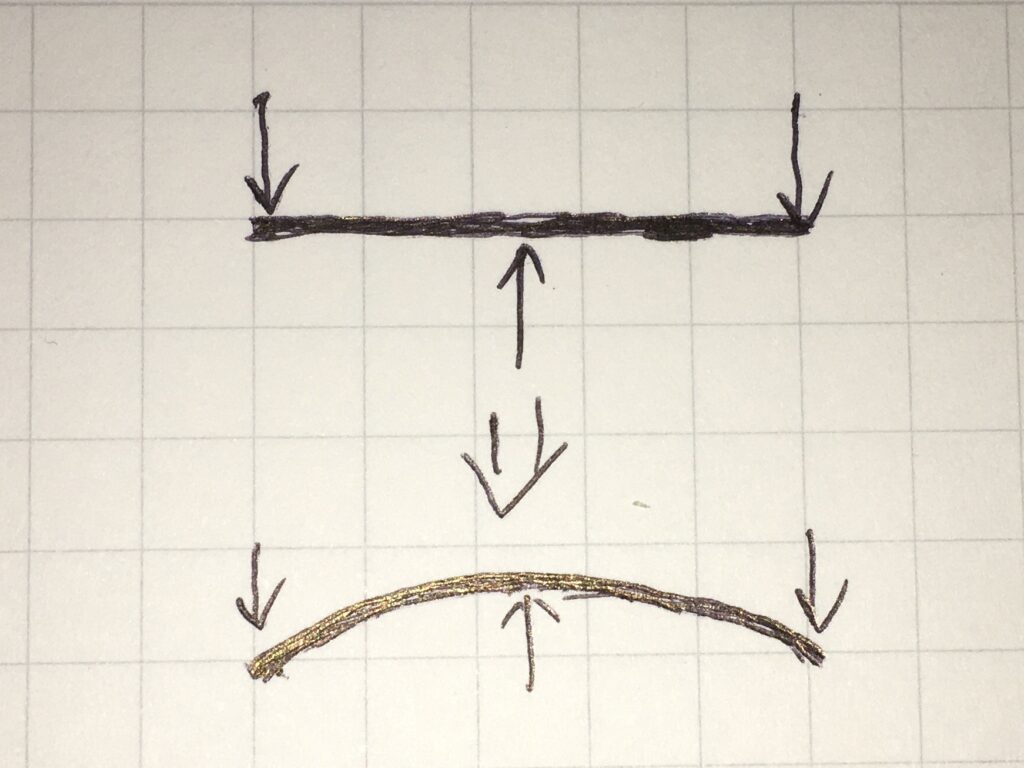
　軸力は、押す・引っ張るのイメージ、曲げモーメントは、曲がる・折れるのイメージ、せん断力は、ちぎれるのイメージが妥当です。

応力の計算のコツ

　ここからは、応力の計算方法について考えていきます。

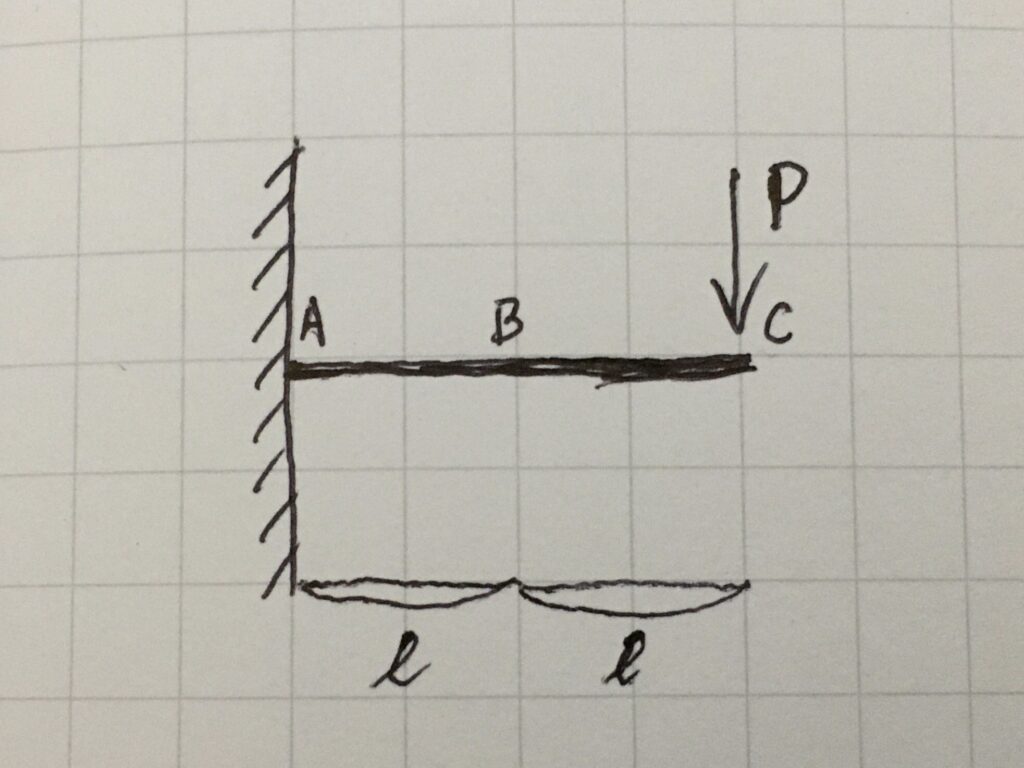
　長さが２ℓの片持ち梁の先端に大きさPの力がかかっているとき、点Ｂにかかる応力を考えます。

　まずは、必ず壁からの反力を考えます。

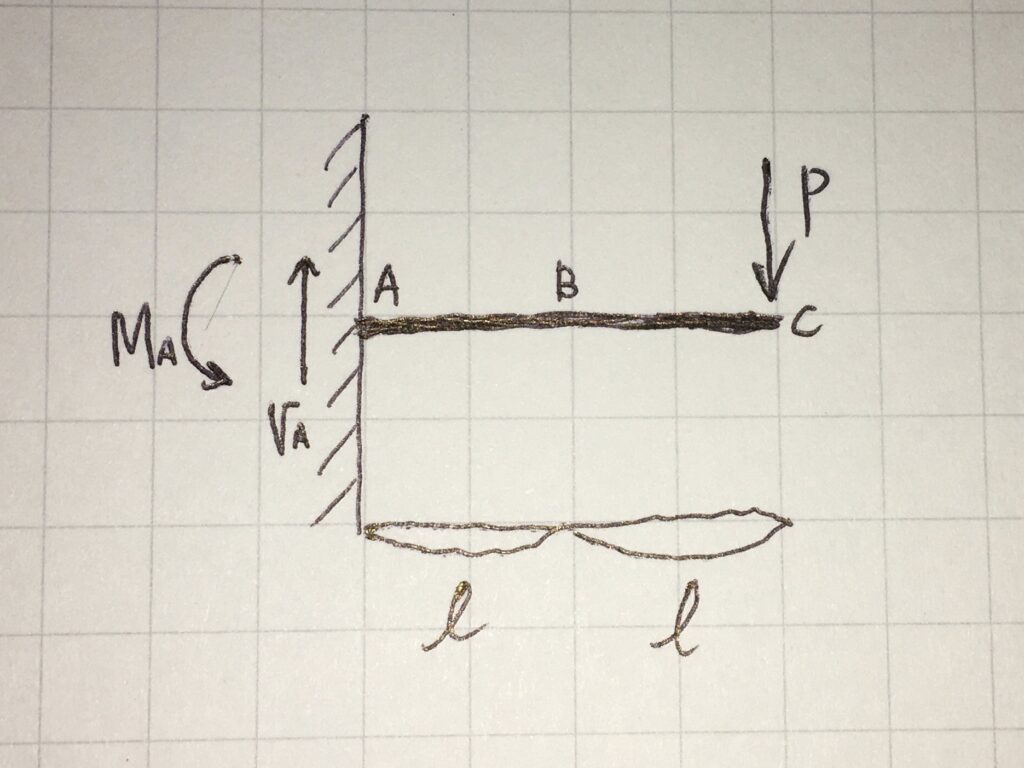
　上図の、反力 VAと、反力モーメントMAの大きさを計算します。

　前の章でも説明しましたが、反力を求めるには、

• 横方向の力のつり合い（今回は横方向の力がないため省略）
• 縦方向の力のつり合い
• モーメントのつり合い

　の計算をします。

縦方向の力のつり合い
（＋VA）＋（-P）＝０
よって、VA＝P

モーメントのつり合い（A点を中心としたモーメントのつり合い）
（＋MA）＋【-（P×２ℓ）】＝０
よって、MA＝２Ｐℓ

　片持ち梁が壁から受ける反力と反力モーメントが求まりました。応力を求めるときは、必ず最初に壁や地面から部材が受けている反力を計算します。

　これを図に反映すると・・・↓

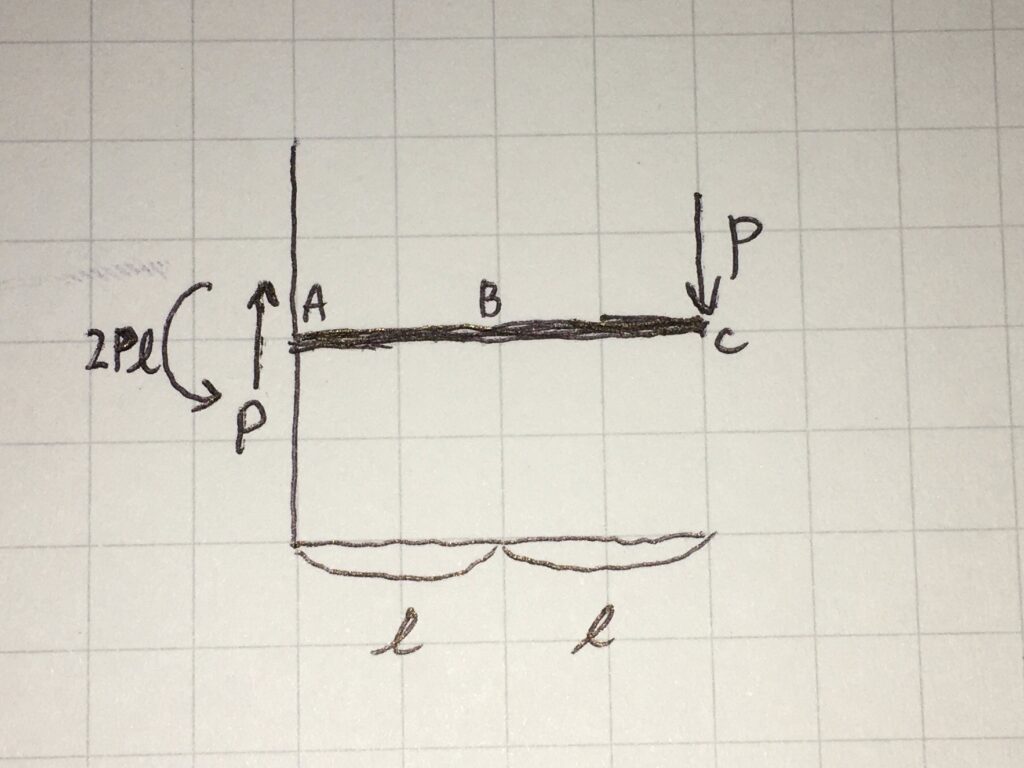
　ここから、点Bに生じる応力を計算しますが、応力を求めたい点（今回は点B）で、部材を切断して考えます。点Bで切断した後に、切る前と同じ強度となるように強力に接着したようなイメージです。

　切断したので、点Aから点Bまで（部材ABと呼びます）と、点Bから点Cまで（部材BCと呼びます）は別の部材と考えます。部材ABと部材BCが、点Bでつながっていると考えるのです。

　わかりやすいように部材ABと部材BCを別の色としてみました↓

　

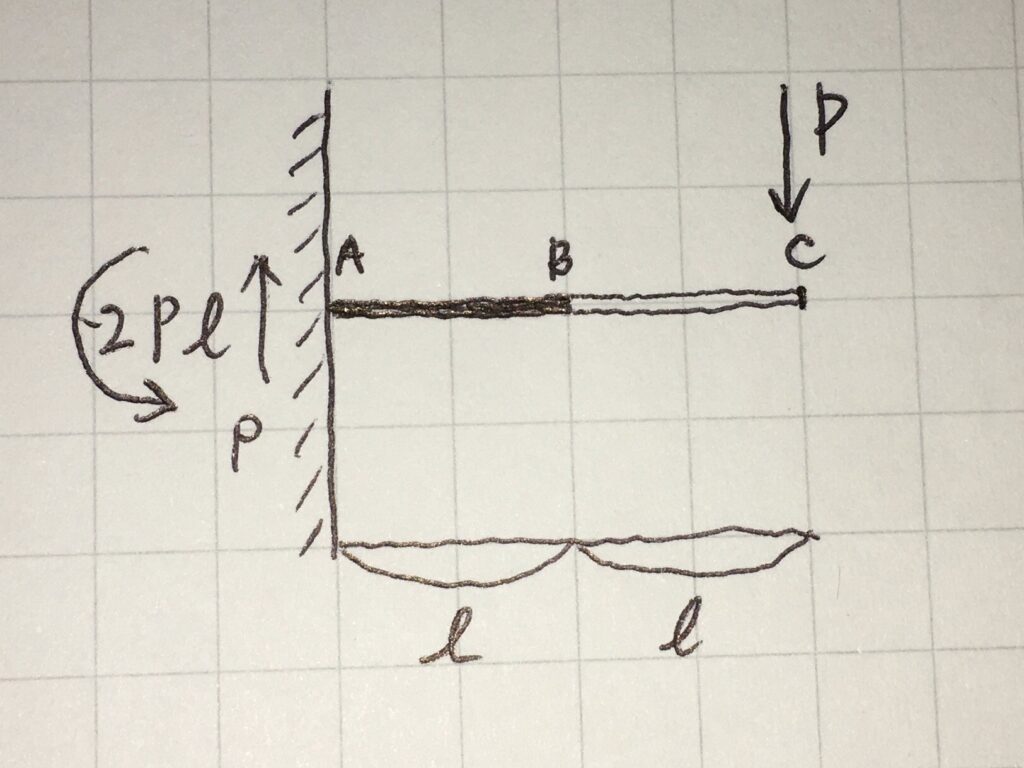
　下図で、部材ABだけ抜き出してみました。

　部材ABの点Aには、壁から、大きさPの反力と、大きさ２PLの反力モーメントがかかっています。さっき計算しましたね。

　同じように、部材ABの点Bにも、部材BCから、力とモーメントがかかっています。壁から部材ABに対して力がかかっているのと同じように、部材BCからも部材ABに対して力がかかっているのです。それらの力を仮に、軸力NB、せん断力QB、曲げモーメントMBと置いて、その大きさを計算していきます。

　

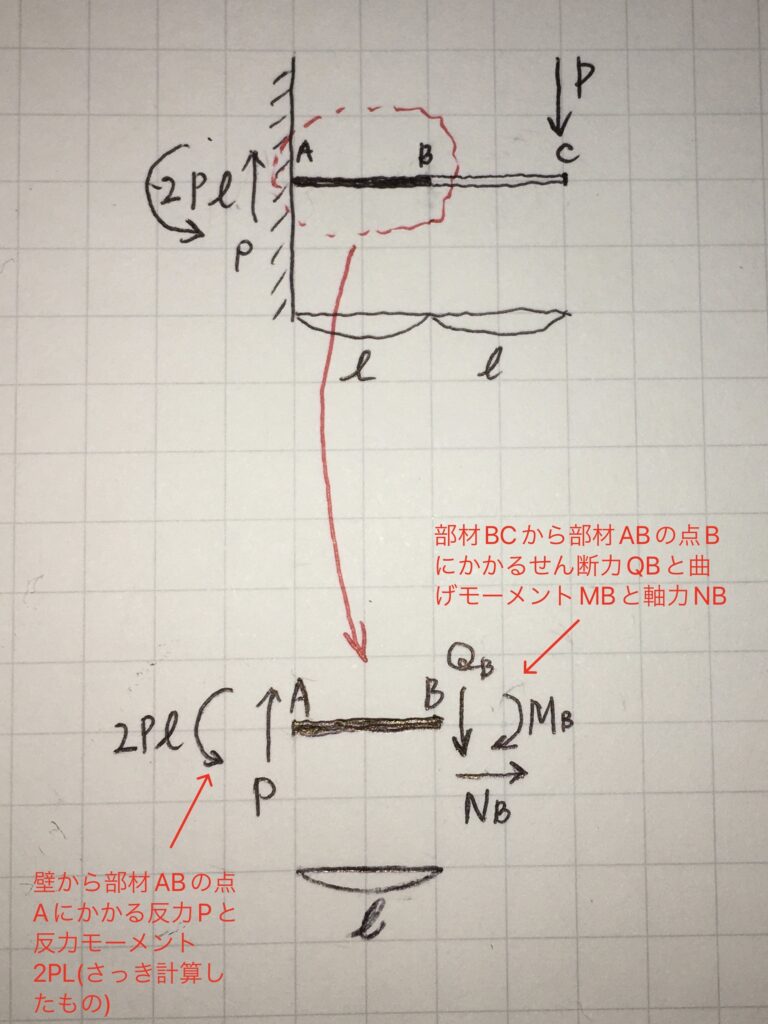
　部材ABは動いていない→力がつり合っているということなので、

• 横方向の力のつり合い
• 縦方向の力のつり合い
• モーメントのつり合い

を考えていきます。

横方向の力のつり合い
NB＝０

縦方向の力のつり合い
（＋P）＋（-QB）＝０
よって、QB＝P

モーメントのつり合い（B点を中心としたモーメントのつり合い）
（＋２Pℓ）＋【-（P×ℓ）】＋（-MB）＝０

よって、MB＝Pℓ

　これらのことから、点Bには、大きさPのせん断力、大きさPℓの曲げモーメントが発生しており、軸力は０（発生していない）ということが分かりました。

　これが、応力の計算の手順です。

　これが構造力学の基本のキになる、一番基本的な考え方です。

　正直この考えが理解できなかったら伸び悩むし、理解できたら構造力学はイージーモードです。

曲げモーメント図をかくときのポイント

　さっきは点Bの曲げモーメントを求めましたが、部材の全ての点について、生じている曲げモーメントを表現した図を曲げモーメント図と言います。

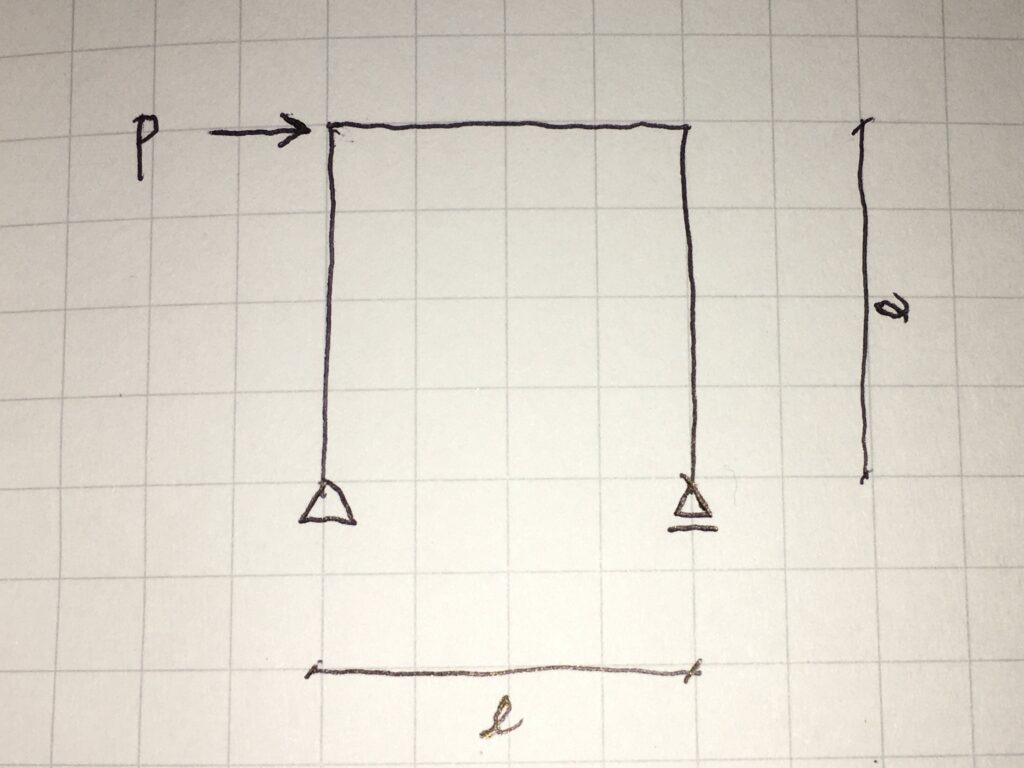
　上図の、水平方向の力Pがかかっているラーメン架構（柱と梁がしっかり接合されている架構）について、曲げモーメント図の例を紹介します。

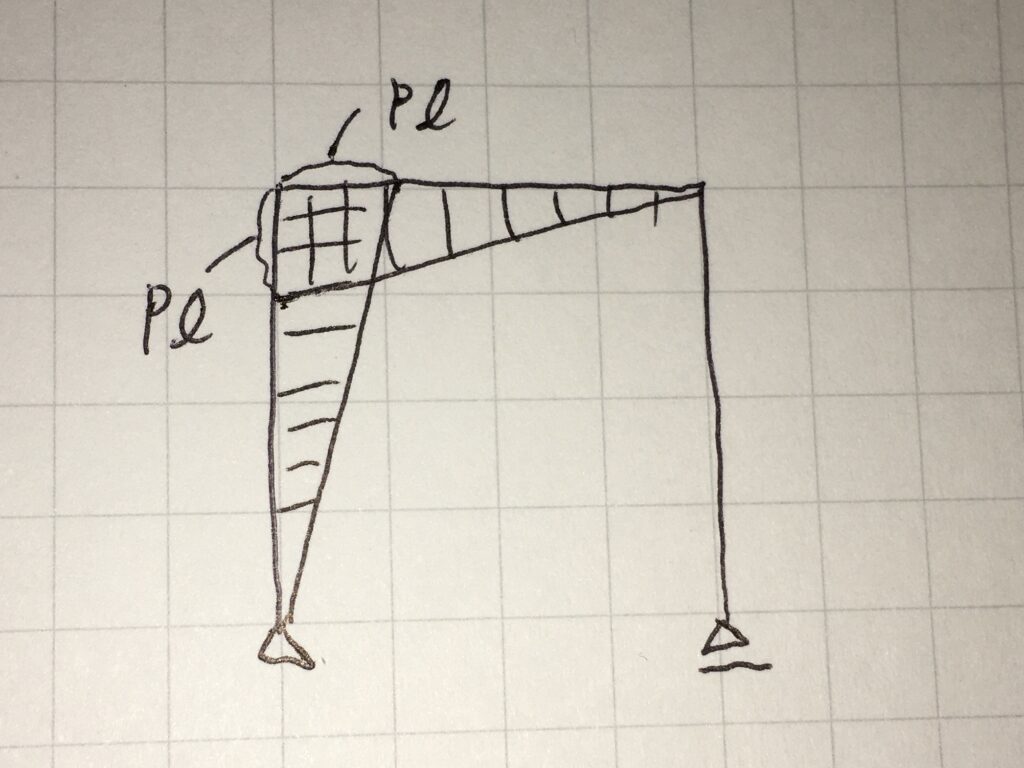
　上図が曲げモーメント図です。この曲げモーメント図からわかることは、以下の通りです。

• 柱脚部分（地面と接している部分）は、ピン接合、ローラー接合であるため、曲げモーメントが0となっている。
• 左部の垂直部材と上部の水平部材が接合している部分が、最も大きな曲げモーメント（大きさPℓ）が生じている。etc

　このように、曲げモーメント図から、部材のどの部分にどのくらいの曲げモーメントがかかっているのかを読み取ることができます。

　ここから、曲げモーメント図を描くときのポイントを紹介します。

　下図のラーメン架構（柱と梁がしっかり接合されている架構）について、モーメント図を描いていきます。　

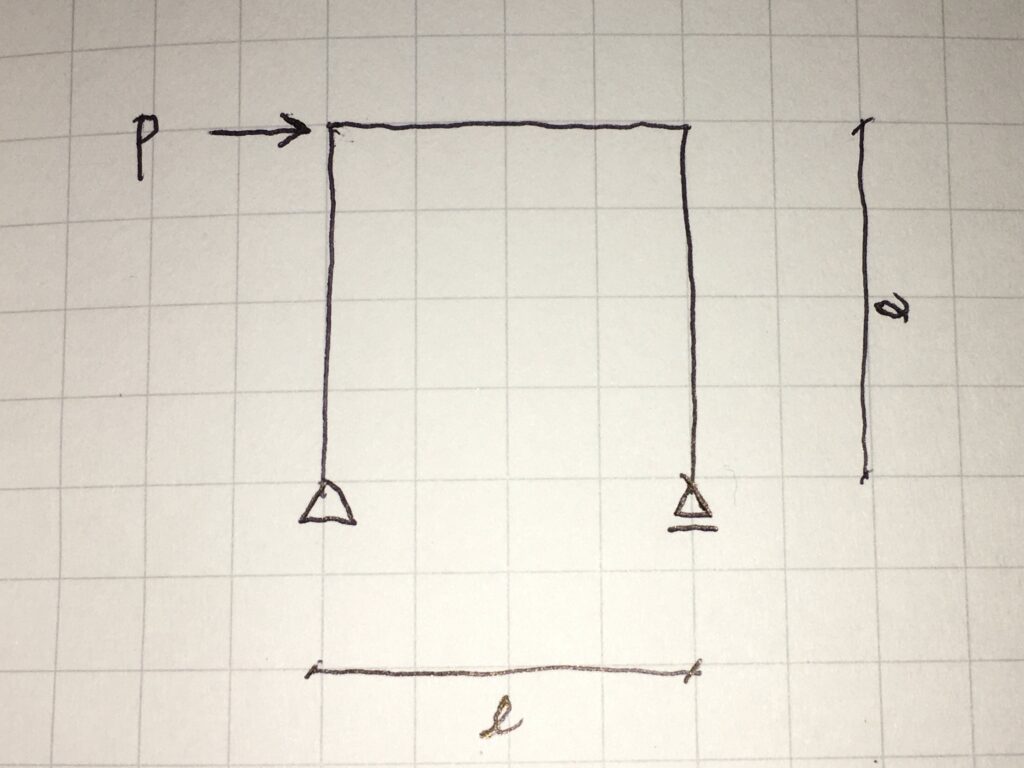
　ラーメン架構の左上の部分に、大きさPの、右向きの力がかかっている状態です。

壁や地面からの反力を求める

　モーメント図を描くときも、まずは地面からの反力を求めます。

• 横方向の力のつり合い
• 縦方向の力のつり合い
• モーメントのつり合い

　これらの力のつり合いから反力を求めると、下図のようになります。

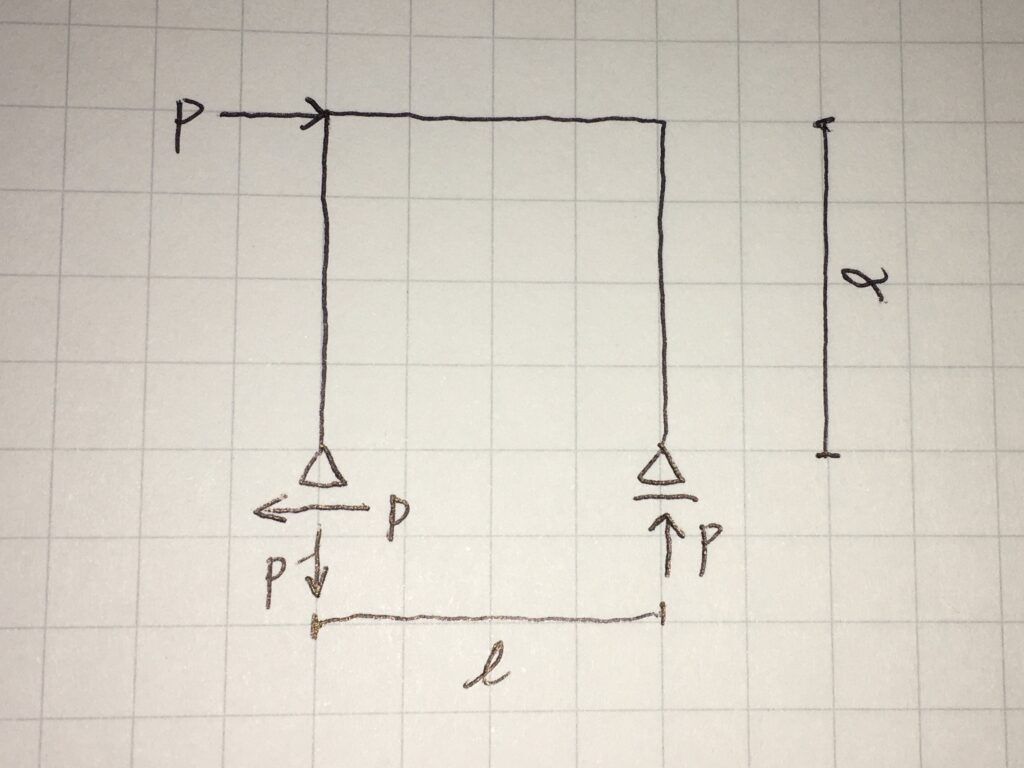
各部材のせん断力を求める

　反力を計算して、書き込んだら、次は各部材に生じるせん断力を計算していきます。

　モーメント図を描きたいのに、なんでせん断力を求めるの？と思う人もいるでしょう。せん断力を先に求めるのは、せん断力がモーメント図の傾きとなるからです。ピンと来ないかもしれませんが、読み進めていただければ分かると思います。

　部材を切断して、力のつり合いから、せん断力を考えると・・・

• 左部の垂直部材に生じるせん断力の大きさはP
• 上部の水平部材に生じるせん断力の大きさはP
• 右部の垂直部材に生じるせん断力の大きさは０（せん断力が生じない）

ということがわかります。

　せん断力を求めたら、次はいよいよモーメント図を描いていきます。

曲げモーメント図を描く

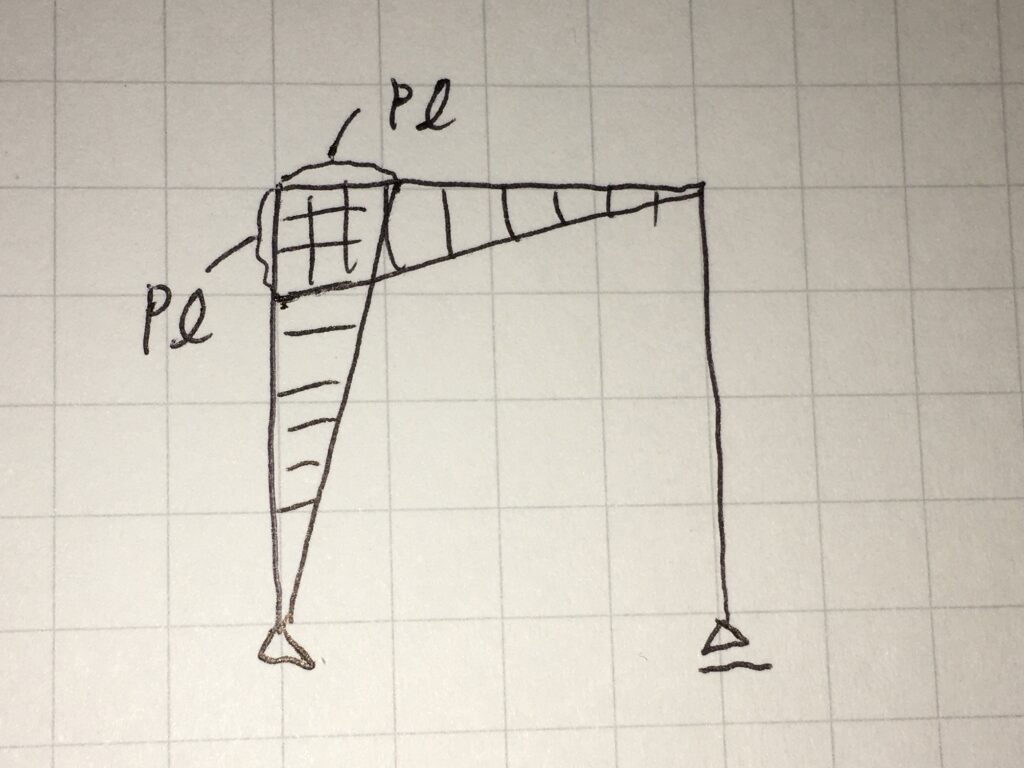
　完成したモーメント図は、上図のようになります。

　モーメント図を描くときのポイントは以下の通りです。覚えてください。

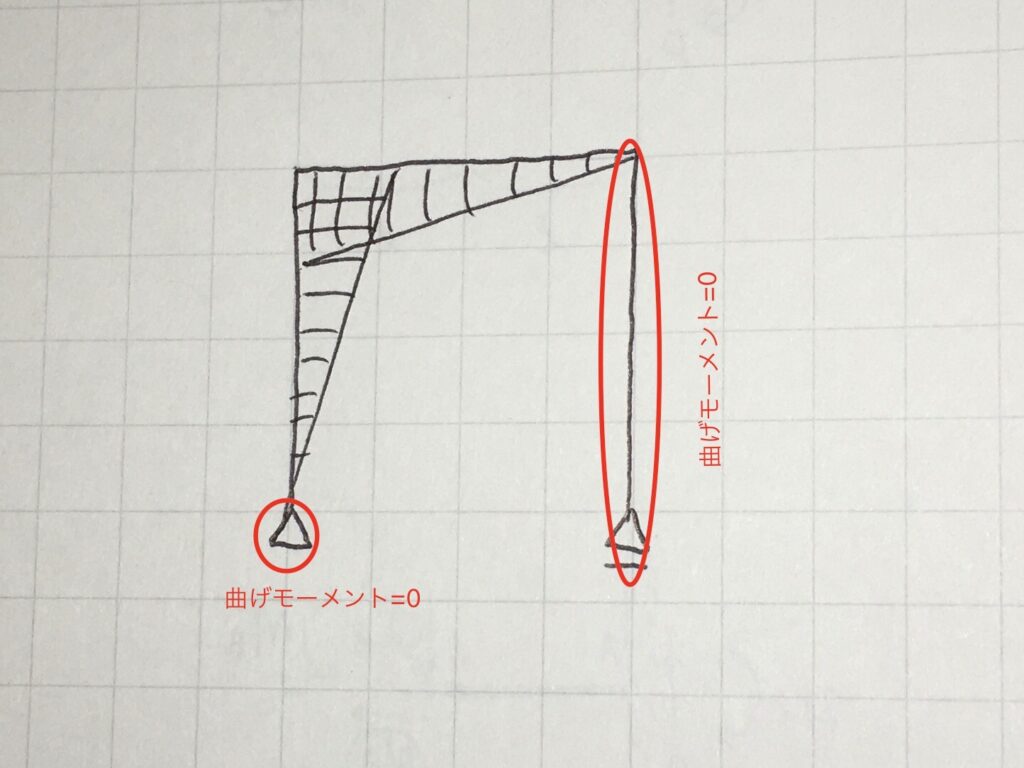
　まず、最初に、曲げモーメント＝０となる場所を探しましょう。ピン接合やローラー接合の場所では曲げモーメント＝0となります。（上図に、曲げモーメント＝０となる場所を示しました）

　また、ローラー支持されている右部の垂直部材についても、曲げモーメント＝０となります。曲げモーメントが生じる部材は曲がりますが、右部の垂直部材は、下端がローラー支持されており左右に自由に動くので、曲がりません。曲がらないということは曲げモーメントが発生していないということです。直感的には分かりにくいかもしれませんが、右部の垂直部材を任意の点で切って、力のつり合いから曲げモーメントを計算してみると、どこで切っても曲げモーメント＝０となることが分かると思います。

　曲げモーメント＝０となる場所が分かったら、次は部材の曲がり方をイメージします。

　

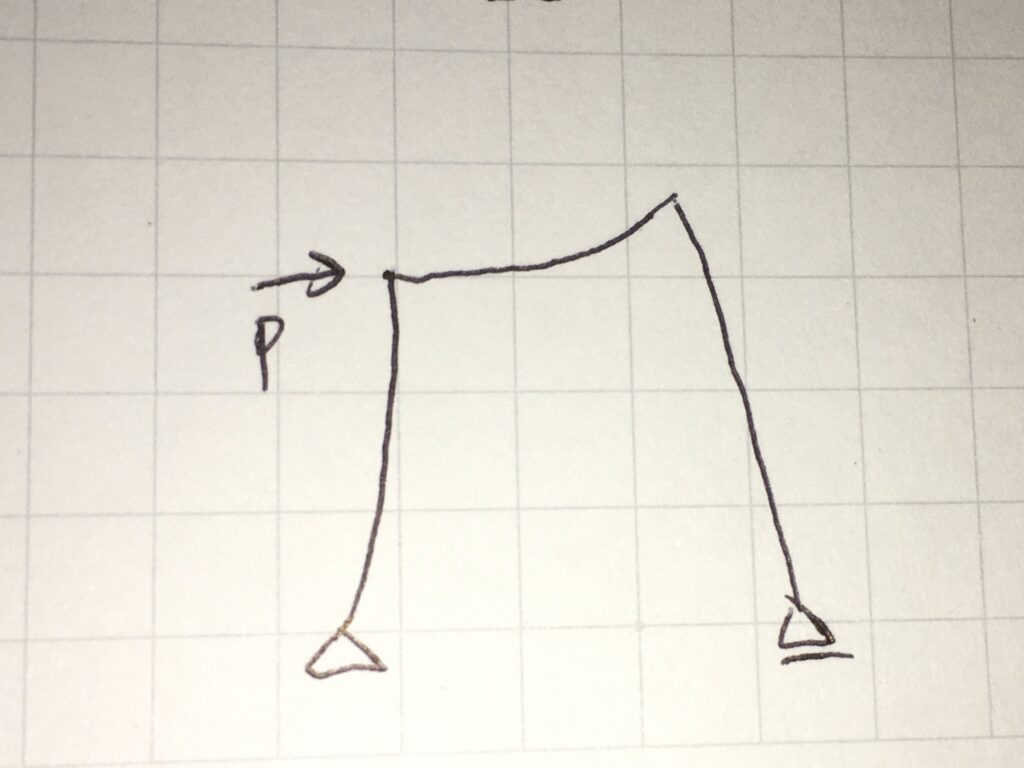
　上図のような曲がり方がイメージできると思います。

　左部の垂直部材は右側に反って曲がり、上部の水平部材は下側に反って曲がります。

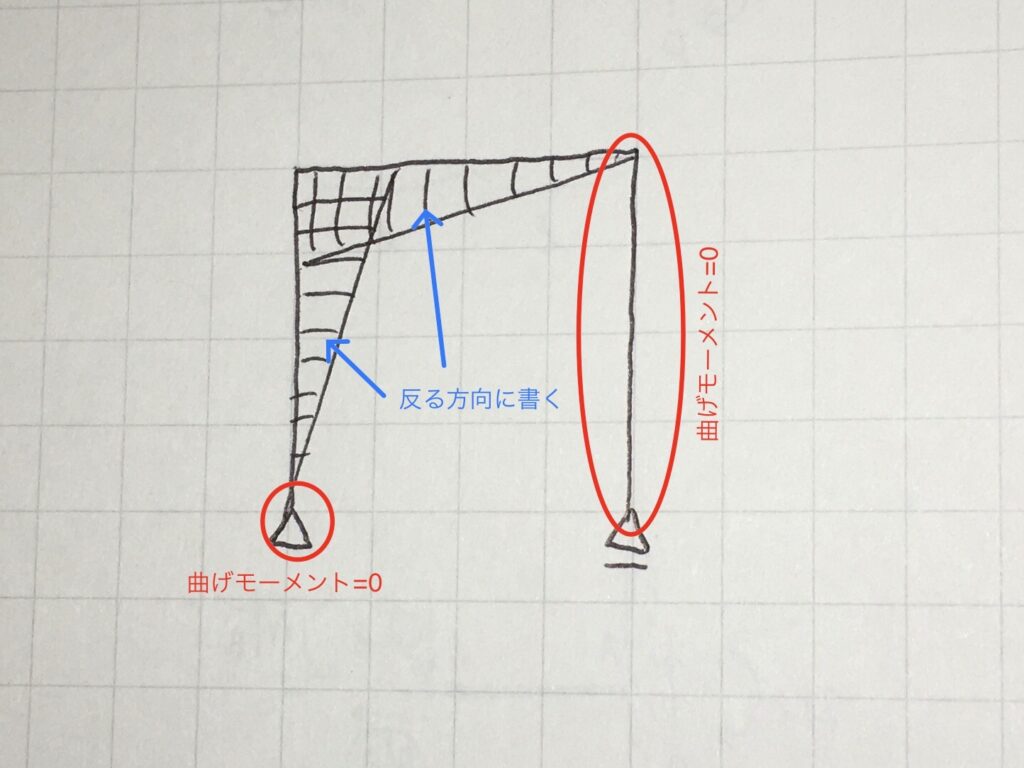
　曲げモーメント図は反っている方に描くので、曲げモーメント＝０となる部分を考慮すると、上図のような図が描けます。今回は、外力が集中荷重のみであるため、曲げモーメント図は直線状となっています。

　最後に、曲げモーメント図の傾き＝せん断力であることを考えると、上部の水平部材と左部の垂直部材の接合部の曲げモーメントがPℓであることが分かります。上部の水平部材と左部の垂直部材の接合部は、左部の垂直部材の柱脚（曲げモーメント＝０）から長さℓだけ離れているので、ℓ×P（傾き）＝Pℓとなります。こうして完成した図が、上図です。

　完成したモーメント図を見ると、一番先に折れそうな場所に、一番大きな曲げモーメントが生じていることが分かると思います。

硬さと強さは違う！硬いものほど多くの荷重を負担する！

構造を勉強する上で、部材の”硬さ”と、部材の”強さ”は、明確に区別しないといけません。

文章題でよく引っ掛けようとしてきます。

硬くても強いとは限らないし、強くても硬いとは限りません。

ピアノ線とガラスを想像してください。

ピアノ線はしなやかに曲がりますが、ちぎれにくいですよね。

一方、ガラスは硬いけど、すぐ割れますよね。

強さと硬さが関係ないなら、構造設計で強さだけ気にしてたら良くね？と思う人もいるでしょう。

なぜ硬さも大事なのかもいうと、硬い部材ほど多くの力がかかるからです。

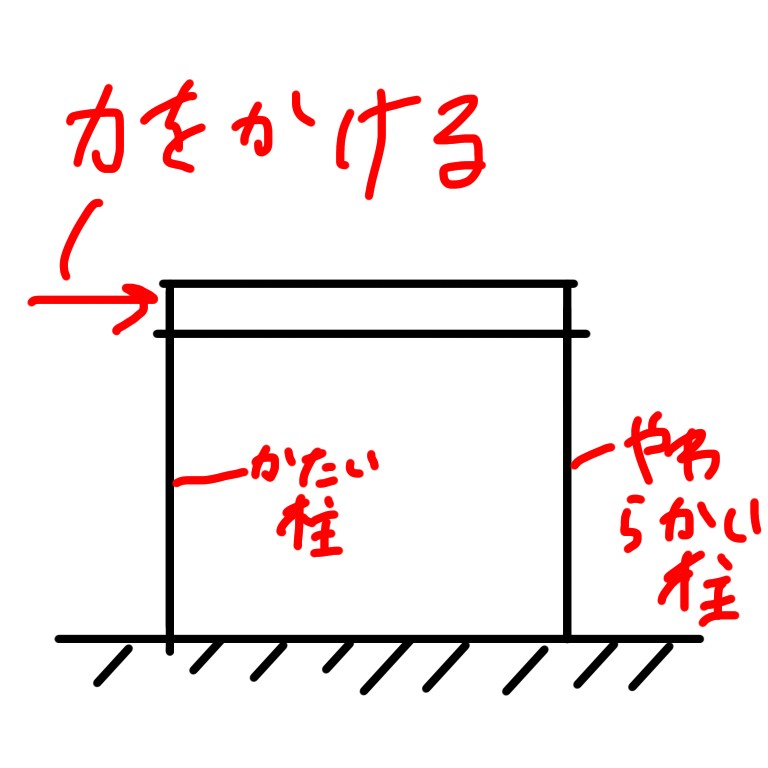
上図のような場合、硬い柱とやわらかい柱の強さが同じだとすると、先に折れるのは硬い柱になります。なぜなら硬い柱の方に大きな力がかかるためです。

やわらかい柱の硬さを1、硬い柱の硬さを4とすると、硬い柱には、柔らかい柱の4倍の力がかかりますので、硬い柱の方を強くしておいた方が安心というわけです。

また、硬さは座屈のしやすさにも影響します。

硬い部材ほど、強い力をかけても座屈が生じにくいです。

針金を両側から押すと、ボヨーンってなりますよね。

これを座屈と言い、座屈が起きると何かと面倒なので、座屈が起きないくらいの硬さで、部材は設計されます。

下の階ほど大きな力がかかる！（上の階の荷重が加わるため）。よって、下の階ほど大きな地震力を受ける

ここも、文章題でよく狙われるポイントです。

地震の時、下図のように、屋上の床にP3、3階床にP2、2階床にP1の力がかかっているとします。

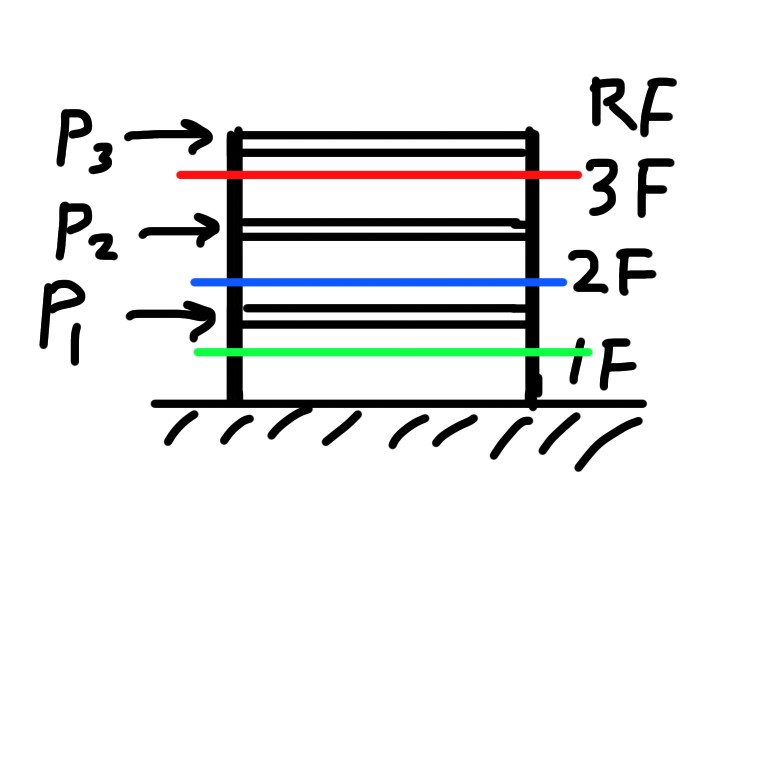
ここで、赤・青・緑の線で部材を切断して考えると力のかかり方は下図のようになります。本来ならモーメントの吊り合いも考えますが、今回省略します。

赤で切った時↓

　横方向の力のつり合いを考えると、3階の柱にかかるせん断力は、以下のようになります。

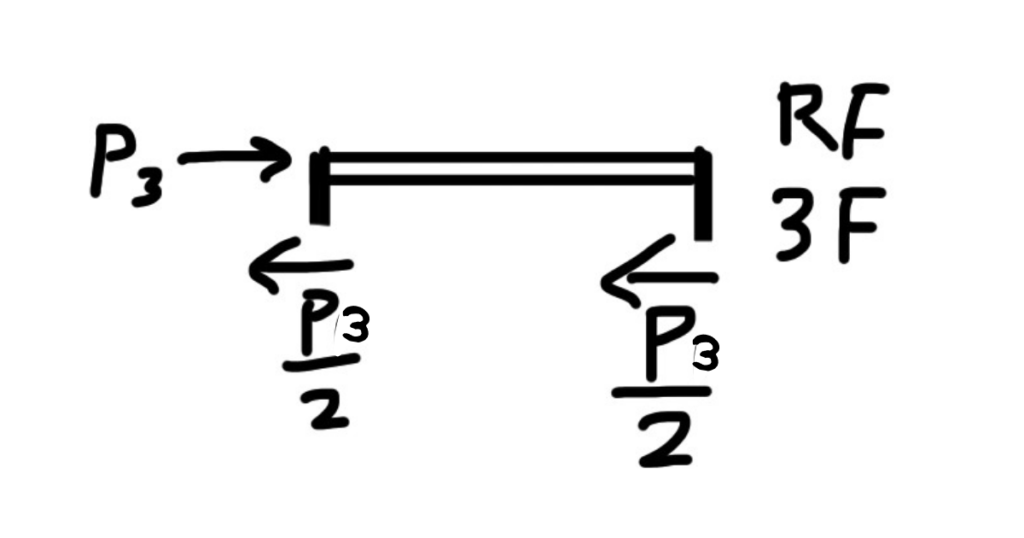
青で切った時↓

　横方向の力のつり合いを考えると2階の柱にかかるせん断力は、以下のようになります。

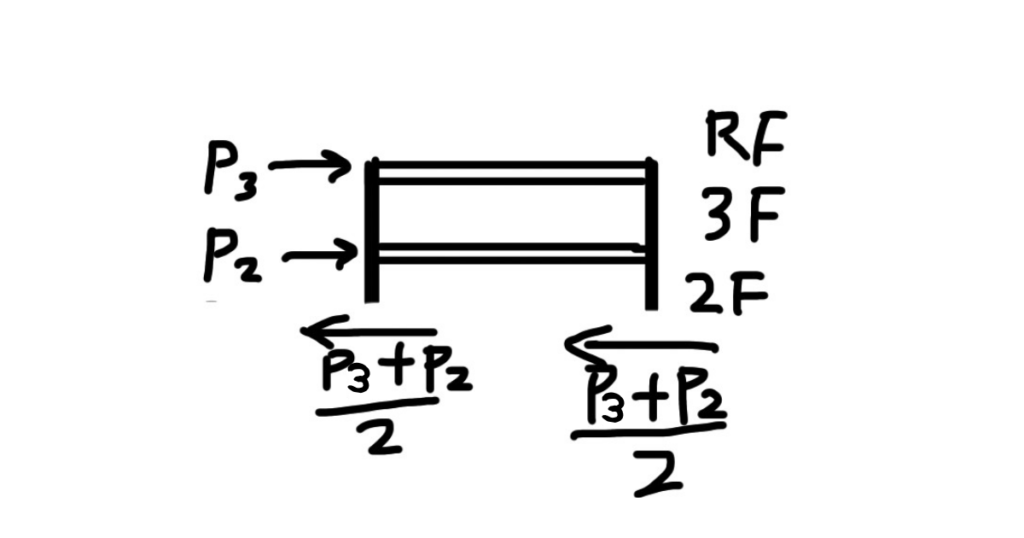
緑で切った時↓

　　横方向の力のつり合いを考えると１階の柱にかかるせん断力は、以下のようになります。

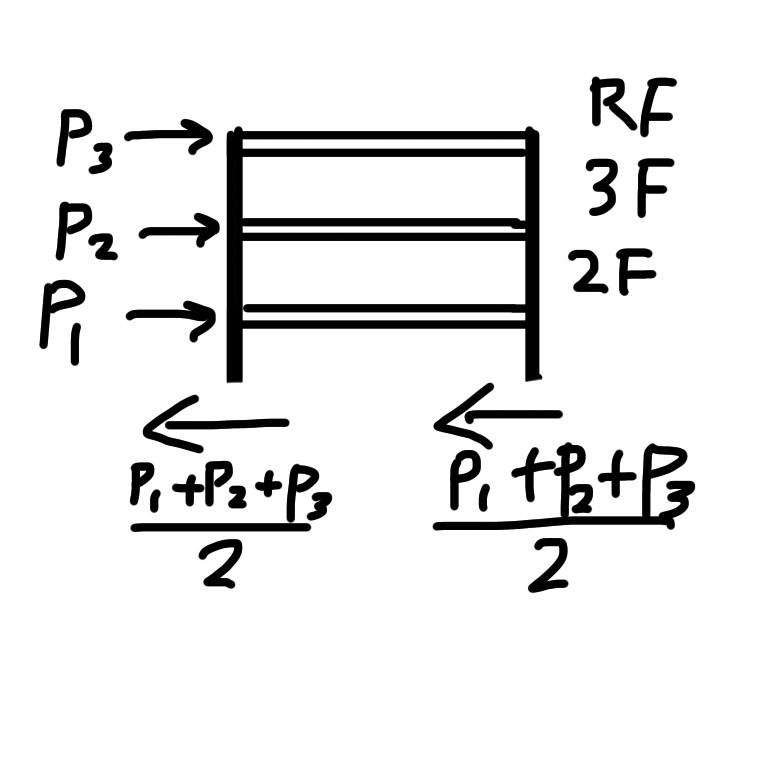
下の階の柱ほど大きな力を受けることがわかると思います。

力学の知識とリンクさせる　

構造の文章題の多くの問題は、構造力学の知識とリンクさせることで正答することができます。

構造力学の知識とリンクさせることで、暗記する量も減らすことができます。

文章題の点数を上げるためにも、構造力学の計算問題は、全問正解できる程度の実力になるまで、練習しておくのをお勧めします。

まとめ

一級建築士の独学には、模試の活用が重要です。模試についての記事もあるので参考にしてください。

【一級建築士　独学】模試を受けよう！メリットと注意点を解説

「一級建築士試験の模試について知りたい」、「一級建築士試験の模試を受けたら点数が悪かった、、、」といった方に向けた記事です。一級建築士試験の模試を受けるメリット、模試の種類と難易度、模試を受けた後にすべきことを解説します。

kenchikuojisan-dokugaku.com

2021.03.28